题目内容
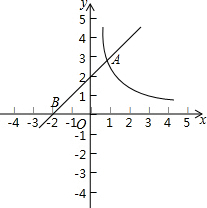 如图,一次函数y1=kx+2的图象与x轴交于点B(-2,0),与函数y2=
如图,一次函数y1=kx+2的图象与x轴交于点B(-2,0),与函数y2=| m |
| x |
(1)求k和m的值;
(2)将函数y2=
| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把B坐标代入一次函数解析式中求出k值,确定出反比例解析式,将A标代入反比例解析式求出a值,确定出A标,将A坐标代入反比例析式求出m的值;
(2)根据函数图象的变化规律可得变换后得到的图象对应的函数解析式为 y=
-3,设△BCD的底BC为n,高为h,则C点的坐标为(n-2,0),将C的坐标代入可得n的值3,根据△BCD的面积是3可求得h=2,从而求得D的坐标.
(2)根据函数图象的变化规律可得变换后得到的图象对应的函数解析式为 y=
| 3 |
| x |
解答:解:(1)根据题意,将点B(-2,0)代入y1=kx+2,
∴0=-2k+2.
∴k=1.
∴A(1,3).
将其代入y2=
,
可得:m=3.
(2)点D的坐标是(
,2)或(3,-2).
∴0=-2k+2.
∴k=1.
∴A(1,3).
将其代入y2=
| m |
| x |
可得:m=3.
(2)点D的坐标是(
| 3 |
| 5 |
点评:此题考查了反比例函数与一次函数的交点问题,利用了待定系数法与数形结合的数学思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
 如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且AD平分∠BAC.
如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且AD平分∠BAC. 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕DE,则AE的长为
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕DE,则AE的长为