题目内容
为绿化校园,我区某学校计划购进甲、乙两种树苗共36棵,已知甲种树苗每棵50元,乙种树苗每棵40元.
(1)若购进甲、乙两种树苗刚好用去1640元,问购进甲、乙两种树苗各多少棵?
(2)若购买甲种树苗的数量不少于乙种树苗的数量2倍,请你选出一种费用最省的方案,并求出该方案所需费用.
(1)若购进甲、乙两种树苗刚好用去1640元,问购进甲、乙两种树苗各多少棵?
(2)若购买甲种树苗的数量不少于乙种树苗的数量2倍,请你选出一种费用最省的方案,并求出该方案所需费用.
考点:一元一次不等式的应用,二元一次方程组的应用
专题:
分析:(1)设购进甲树苗x棵,艺树苗y棵.等量关系:甲、乙两种树苗共36棵;甲、乙两种树苗刚好用去1640元;
(2)不等关系为:甲种树苗的数量不少于乙种树苗的数量2倍.
(2)不等关系为:甲种树苗的数量不少于乙种树苗的数量2倍.
解答:解:(1)设购进甲树苗x棵,乙树苗y棵.则
,
解得
.
答:购进甲、乙两种树苗分别是20棵、16棵;
(2)设购进甲树苗a棵,则购进的乙树苗为(36-a)棵,所需费用为w.
依题意得 x≥2(36-a)
解得 a≥24.
所以24≤a≤36.
则w=50a+40(36-a)=6x+1440.
因为6>0,
所以函数w=6x+1440的图象是w随a的增大而增大,
所以 当x=24时,w最小=1584
答:购进24棵甲种树苗,12棵乙种树苗所需的费用最低,最低为1584元.
|
解得
|
答:购进甲、乙两种树苗分别是20棵、16棵;
(2)设购进甲树苗a棵,则购进的乙树苗为(36-a)棵,所需费用为w.
依题意得 x≥2(36-a)
解得 a≥24.
所以24≤a≤36.
则w=50a+40(36-a)=6x+1440.
因为6>0,
所以函数w=6x+1440的图象是w随a的增大而增大,
所以 当x=24时,w最小=1584
答:购进24棵甲种树苗,12棵乙种树苗所需的费用最低,最低为1584元.
点评:本题考查一元一次不等式的应用,关键是将现实生活中的事件与数学思想联系起来,读懂题意列出不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+2,y0-1).
如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+2,y0-1). 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.
如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.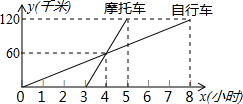 甲、乙两地相距120千米,A骑自行车,B骑摩托车,他们沿相同路线由甲地到乙地行驶,两人行驶的路程y(千米)与时间x(小时)的关系如图,请你根据图象解决下面的问题:
甲、乙两地相距120千米,A骑自行车,B骑摩托车,他们沿相同路线由甲地到乙地行驶,两人行驶的路程y(千米)与时间x(小时)的关系如图,请你根据图象解决下面的问题: 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,则∠ACB的度数为
如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,则∠ACB的度数为