题目内容
立定跳远时,以小明起跳时重心所在竖直方向为y轴(假设起跳时重心与起跳点在同一竖直方向上),地平线为x轴,建立平面直角坐标系(如图),则小明此跳重心所走过的路径是一条形如y=-0.2(x-1)2+0.7的抛物线,在最后落地时重心离地面0.3m(假如落地时重心与脚后跟在同一竖直方向上).
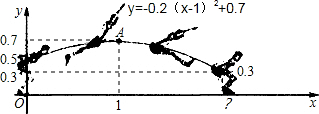
(1)小明在这一跳中,重心离地面最高时距离地面多少米?此时他离起跳点的水平距离有多少米?
(2)小明此跳在起跳时重心离地面有多高?
(3)小明这一跳能得满分吗(2.40m为满分)?
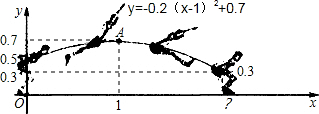
(1)小明在这一跳中,重心离地面最高时距离地面多少米?此时他离起跳点的水平距离有多少米?
(2)小明此跳在起跳时重心离地面有多高?
(3)小明这一跳能得满分吗(2.40m为满分)?
考点:二次函数的应用
专题:
分析:(1)根据抛物线的顶点式可以直接求出结论;
(2)当x=0时,代入解析式求出y的值就可以求出结论;
(3)当y=0.3时代入解析式求出其解即可.
(2)当x=0时,代入解析式求出y的值就可以求出结论;
(3)当y=0.3时代入解析式求出其解即可.
解答:解:(1)∵y=-0.2(x-1)2+0.7,
∴抛物线的顶点坐标为(1,0.7),
∴重心离地面最高时距离地面0.7米,此时他离起跳点的水平距离有1米;
(2)当x=0时,
y=-0.2(0-1)2+0.7=0.5米,
∴小明此跳在起跳时重心离地面有0.5高;
(3)当y=0.3时,
0.3=-0.2(x-1)2+0.7,
解得:x1=1-
(舍去),x2=1+
,
小明的成绩为1+
米.
∵1+
>2.4,
∴小明这一跳能得满分.
∴抛物线的顶点坐标为(1,0.7),
∴重心离地面最高时距离地面0.7米,此时他离起跳点的水平距离有1米;
(2)当x=0时,
y=-0.2(0-1)2+0.7=0.5米,
∴小明此跳在起跳时重心离地面有0.5高;
(3)当y=0.3时,
0.3=-0.2(x-1)2+0.7,
解得:x1=1-
| 2 |
| 2 |
小明的成绩为1+
| 2 |
∵1+
| 2 |
∴小明这一跳能得满分.
点评:本题考查了二次函数的解析式的运用,顶点式的运用,根据解析式由函数值求自变量的值的而运用,根据自变量的值求函数值的运用,解答时灵活运用解析式求解是关键.

练习册系列答案
相关题目
如果
•
=
,那么x应满足的条件是( )
| x |
| x-5 |
| x(x-5) |
| A、x≥0 | B、x≤0 |
| C、0≤x≤5 | D、x≥5 |
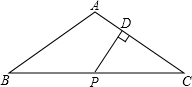 如图,已知:在△ABC中,AB=AC,∠BAC=120°,P为BC边的中点,PD⊥AC.求证:CD=3AD.
如图,已知:在△ABC中,AB=AC,∠BAC=120°,P为BC边的中点,PD⊥AC.求证:CD=3AD. 如图,已知△AOB∽△DOC,OA=2,AD=9,OB=5,DC=12.求AB,OC的长.
如图,已知△AOB∽△DOC,OA=2,AD=9,OB=5,DC=12.求AB,OC的长. 如图,P是面积为
如图,P是面积为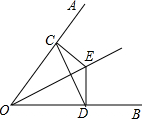 如图,已知E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别是C,D.求证:OE垂直平分CD.
如图,已知E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别是C,D.求证:OE垂直平分CD.