题目内容
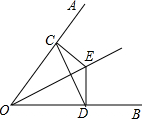 如图,已知E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别是C,D.求证:OE垂直平分CD.
如图,已知E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别是C,D.求证:OE垂直平分CD.考点:角平分线的性质,全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:先根据E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA得出△ODE≌△OCE,可得出OD=OC,DE=CE,OE=OE,可得出△DOC是等腰三角形,由等腰三角形的性质即可得出OE是CD的垂直平分线.
解答:证明:∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴DE=CE,OE=OE,
在Rt△ODE与Rt△OCE中,
,
∴Rt△ODE≌Rt△OCE(HL),
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线.
∴DE=CE,OE=OE,
在Rt△ODE与Rt△OCE中,
|
∴Rt△ODE≌Rt△OCE(HL),
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
 如图,将边长为a的正方形ABCD沿直线l按顺时针方向翻滚,当正方形翻滚一周时,正方形的中心O所经过的路径长为多少?
如图,将边长为a的正方形ABCD沿直线l按顺时针方向翻滚,当正方形翻滚一周时,正方形的中心O所经过的路径长为多少? 已知点P为等边△ABC外一点,且∠BPC=120°,试说明PB+PC=AP.
已知点P为等边△ABC外一点,且∠BPC=120°,试说明PB+PC=AP.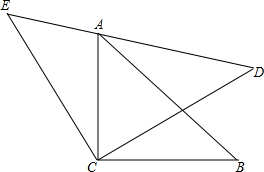 如图,△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2.(提示:连接BD)
如图,△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2.(提示:连接BD) 如图,在?ABCD中,对角线AC,BD交于点O,且E,F分别是BO和DO的中点.求证:AE=CF.
如图,在?ABCD中,对角线AC,BD交于点O,且E,F分别是BO和DO的中点.求证:AE=CF.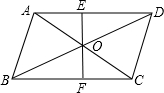 如图,在?ABCD中,对角线AC,BD交于点O,EF过点O,并与AD,BC边分别交于点E,F.如果AB=4,BC=5,OE=1.5,求四边形CDEF的周长.
如图,在?ABCD中,对角线AC,BD交于点O,EF过点O,并与AD,BC边分别交于点E,F.如果AB=4,BC=5,OE=1.5,求四边形CDEF的周长. 把一副直角三角尺按如图所示叠放在一起,其中∠ACB=∠CBD=90°,AC=BC=10,∠BCD=30°,则这副直角三角尺重叠部分的面积为
把一副直角三角尺按如图所示叠放在一起,其中∠ACB=∠CBD=90°,AC=BC=10,∠BCD=30°,则这副直角三角尺重叠部分的面积为