题目内容
15.小芳每次骑车从家到学校都要经过一段坡度相同的上坡路和下坡路,假设她骑车坡度相等的上坡路与下坡路平均速度基本相同,且上坡路骑行50米与下坡路骑行80米所用的时间相等.当她从家到学校时,下坡路的长为400米,下坡路比上坡路多花一分钟,设她骑行下坡路的速度为x米/分钟.(1)用含x的代数式表示她从家到学校时上坡路段的路程.
(2)当她从学校回家时,在这两个坡道所花的时间为10分30秒,请求出她回家时在下坡路段所花的时间.
分析 (1)设出上学时上坡的路程为y米,根据题意找出y与x的关系式,整理即可得出小芳从家到学校时上坡路段的路程;
(2)放学回家正好与上学时从家到学校相反,即上下坡颠倒,根据(1)结合题意算出下坡速度x的值,再结合(1)即可算出小芳回家时在下坡路段所花的时间.
解答 解:(1)设小芳从家到学校时上坡路段的路程为y米,根据题意可得:
$\frac{400}{x}$-1=$\frac{y}{\frac{50x}{80}}$,
整理,得y=-$\frac{5}{8}$x+250,
故小芳从家到学校时上坡路段的路程为-$\frac{5}{8}$x+250米.
(2)∵放学从学校到家正好与上学从家到学校相反,上下坡颠倒,
∴放学回家上坡路程为400米,下坡路程为-$\frac{5}{8}$x+250米,
根据题意,得$\frac{400}{\frac{50x}{80}}$+$\frac{-\frac{5}{8}x+250}{x}$=10.5,
整理,得890-$\frac{5}{8}$x=$\frac{21}{2}$x,
解得:x=80,
下坡所花时间为$\frac{-\frac{5}{8}x+250}{x}$=$\frac{250}{80}$-$\frac{5}{8}$=$\frac{5}{2}$(分)
答:小芳回家时在下坡路段所花的时间为$\frac{5}{2}$分.
点评 本题考查分式方程的应用,解题的关键是明白上学放学路程正好相反,上学的上坡变成放学回家的下坡,上学的下坡变为放学回家的上坡.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2$\sqrt{3}$,则MN的值为9-5$\sqrt{3}$.
如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2$\sqrt{3}$,则MN的值为9-5$\sqrt{3}$. 如图,在矩形ABCD中,DE平分∠ADC,∠EDO=15°.
如图,在矩形ABCD中,DE平分∠ADC,∠EDO=15°. 如图,点O是等边△ABC内的一点.∠BOC=α,将△BOC绕点C按顺时针旋转60°得到△ADC,连接OD.
如图,点O是等边△ABC内的一点.∠BOC=α,将△BOC绕点C按顺时针旋转60°得到△ADC,连接OD. 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是$\sqrt{2}$.
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是$\sqrt{2}$.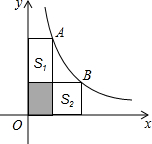 如图,A、B两点在双曲线$y=\frac{12}{x}$上,分别过A、B两点想坐标轴作垂线,若S阴影=3,则S1+S2的值为( )
如图,A、B两点在双曲线$y=\frac{12}{x}$上,分别过A、B两点想坐标轴作垂线,若S阴影=3,则S1+S2的值为( )