题目内容
11. 如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2$\sqrt{3}$,则MN的值为9-5$\sqrt{3}$.
如图,将等腰Rt△GAE绕点A顺时针旋转60°得到△DAB,其中∠GAE=∠DAB=90°,GE与AD交于点M,过点D作DC∥AB交AE于点C.已知AF平分∠GAM,EH⊥AE交DC于点H,连接FH交DM于点N,若AC=2$\sqrt{3}$,则MN的值为9-5$\sqrt{3}$.
分析 作MK⊥AC,FT⊥AD垂足分别为K,T,证明△AGF≌△AEM,△AFT≌△AMK得到AF=AM,FT=MK=EK=DM,在RT△ADC中根据已知条件求出CD,AD,设MK=EK=x,根据AE=AK+EK列出方程求出x,在RT△HEC中求出HC,进而求出DH,再根据$\frac{DH}{FT}=\frac{DN}{NT}$,求出DN,利用MN=AD-AM-DN求出MN.
解答 解:作MK⊥AC,FT⊥AD垂足分别为K,T,
∵Rt△GAE绕点A顺时针旋转60°得到△DAB,
∴∠GAD=∠CAB=60°,
∵∠GAE=∠DAB=90°,AG=AE=AD=AB,
∴∠DAC=30°,∠G=∠AEG=45°,
∵AF平分∠GAD,
∴∠GAF=∠FAT=30°,
在△AGF和△AEM中,
$\left\{\begin{array}{l}{∠G=∠AEM}\\{AG=AE}\\{∠GAF=∠MAE}\end{array}\right.$,
∴△AGF≌△AEM,
∴AF=AM
在△AFT和△AMK中,
$\left\{\begin{array}{l}{∠FAT=∠MAK}\\{∠FTA=∠MKA}\\{AF=AM}\end{array}\right.$,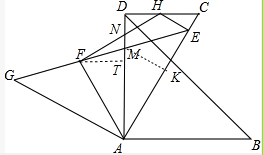
∴△AFT≌△AMK,
∴AT=AK,
∵AD=AE,
∴DT=EK,
∵∠KME=∠KEM=45°,
∴MK=EK=DT=FT,
设MK=KE=x,则AK=$\sqrt{3}$x,
∵$AC=2\sqrt{3}$,∠DAC=30°,
∴$DC=\sqrt{3}$,AD=3,∴AE=AD=3,
∴x+$\sqrt{3}$x=3
x=$\frac{3(\sqrt{3}-1)}{2}$,
∴DT=FT=MK=EK=$\frac{3(\sqrt{3}-1)}{2}$,AM=3($\sqrt{3}$-1),EC=2$\sqrt{3}$-3,
在RT△HEC中,∵∠C=60°,EC=2$\sqrt{3}$-3,
∴HC=2EC=4$\sqrt{3}$-6,DH=DC-HC=$\sqrt{3}$-(4$\sqrt{3}$-6)=6-3$\sqrt{3}$,
设DN=y,∵DH∥FT,
∴$\frac{DH}{FT}=\frac{DN}{NT}$,
∴$\frac{6-3\sqrt{3}}{\frac{3(\sqrt{3}-1)}{2}}=\frac{y}{\frac{3(\sqrt{3}-1)}{2}-y}$,
∴y=2$\sqrt{3}$-3,
∴MN=AD-AM-DN=3-3($\sqrt{3}$-1)-(2$\sqrt{3}$-3)=9-5$\sqrt{3}$.
点评 本题考查旋转性质、全等三角形的判定和性质、勾股定理、平行成比例等知识,灵活运用全等三角形的性质是解题的关键.

| A. | 4m-m=3 | B. | 2m2+3m3=5m5 | C. | xy+xy=2xy | D. | -(m+2n)=-m+2n |
| A. | 16xy | B. | 4xy | C. | 16x+y | D. | 22(x+y) |
| A. | 四边相等的四边形是正方形 | |
| B. | 对角线垂直的平行四边形是正方形 | |
| C. | 一组对边平行的四边形是平行四边形 | |
| D. | 有一个角是直角的平行四边形是矩形 |
 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若CD=2EF=6,BC=6$\sqrt{2}$,则∠C等于45°.
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若CD=2EF=6,BC=6$\sqrt{2}$,则∠C等于45°. 如图,已知AD∥BC.
如图,已知AD∥BC.