题目内容
如图,在△ABC中,∠A=90°,AB=AC=12 cm,半径为4 cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1 cm/s、x cm/s、1.5 cm/s,运动时间为t s.
(1)求证:BD=CE;
(2)若x=3,当△PBQ∽△QCR时,求t的值;
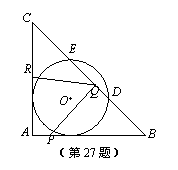 (3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
(3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
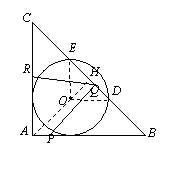
(1)证明:连接AO并延长交BC于点H.连接OE、OD.
∵⊙O与AB、AC两边都相切,
∴点O到AB、AC两边的距离相等.
∴AH是∠CAB的平分线.
∵AB=AC,
∴AH⊥BC,AH平分BC.
∵OE=OD,OH⊥ED,
∴OH平分ED.
∵CE=CH-EH,BD=BH-DH,
且CH=BH,EH=DH,
∴ BD=CE. 3分


(2)解:在Rt△ABC中,BC=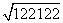 =12
=12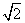 .
.
∵△PBQ∽△QCR,∴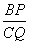 =
=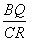 ,即
,即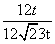 =
=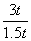 .解得t=
.解得t=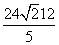 . 6分
. 6分
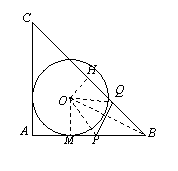
(3)解:设⊙O与AB相切于点M,连接OM、OB、OP、OQ,H参考(1)中作法.
∵点O与点B关于PQ对称,
∴PQ垂直平分BO.
∴OP=BP,OQ=BQ.
∵⊙O与AB相切于点M,∴OM⊥AB.
设BP=a,在Rt△OMP中,(12-4-a)2+42=a2,解得a=5;
设BQ=b,在Rt△OHB中,(6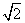 -b)2+(2
-b)2+(2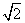 )2=b2,解得b=
)2=b2,解得b=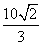 .
.
t=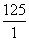 =7 s. x=
=7 s. x=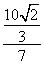 =
=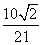 cm.
cm.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
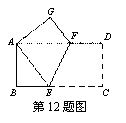
暑假衔接培优教材浙江工商大学出版社系列答案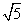 D.AF=EF
D.AF=EF