题目内容
已知二次函数y=x2-ax-2a2(a为常数,且a≠0).
(1)证明该二次函数的图像与x轴的正半轴、负半轴各有一个交点;
(2)若该二次函数的图像与y轴的交点坐标为(0,-2),试求该函数图像的顶点
坐标.
解:(1)
法一:y=x2-ax-2a2 =(x+a)(x-2a),
令y=0,则x1=-a,x2=2a, …………2分
∵a≠0,x1、x2的值必为一正一负, …………3分
∴该二次函数的图像与x轴的正半轴、负半轴各有一个交点; …………4分
法二:由y=0得:x2-ax-2a2 =0(*),
∵△=(-a)2-4×1×(-2a2)=9a2,a≠0,
∴△>0,∴(*)有二个不相等的值数根.设二实数根为x1,x2,…………2分
∵x1x2=-2a2<0,∴(*)有2个异号的实数根
∴该二次函数的图像与x轴的正半轴、负半轴各有一个交点;…………4分
(2)由题意,得-2a2=-2 ,所以a=1或-1. …………5分
当a=1时,y=x2-x-2=(x-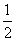 )2-
)2-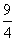 ,顶点坐标为(
,顶点坐标为(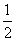 ,-
,-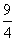 ) …………6分
) …………6分
当a=-1时,y=x2+x-2=(x+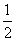 )2-
)2-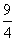 ,顶点坐标为(-
,顶点坐标为(-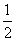 ,-
,-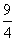 )…………7分
)…………7分
该函数图像的顶点坐标为(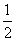 ,-
,-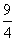 )或(-
)或(-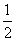 ,-
,-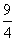 ).…………8分
).…………8分

练习册系列答案
相关题目
 的图象相交于点A(-1,2)和点B .
的图象相交于点A(-1,2)和点B . -
- = .
= .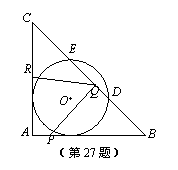 (3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
(3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.