题目内容
如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.
(1)求证:AE=CG;
(2)试判断BE和DF的位置关系,并说明理由.
 |
解:(1)证明:在正方形ABCD中,
∵AD=CD,
∴∠DAE=∠DCG,
∵DE=DG, ∴∠DEG=∠DGE,
∴∠AED=∠CGD.
在△AED和△CGD中,
∵∠DAE=∠DCG,∠AED=∠CGD,DE=DG,
∴△AED≌△CGD,
∴AE=CG. 4分
(2)解法一:BE∥DF,理由如下:
在正方形ABCD中,AB∥CD,AB=CD,
∴∠BAE=∠DCG.
又∵AE=CG,
∴△AEB≌△CGD,
∴∠AEB=∠CGD.
∵∠CGD=∠EGF,
∴∠AEB=∠EGF,
∴ BE∥DF. 9分
解法二:BE∥DF,理由如下:
在正方形ABCD中,
∵AD∥FC,
∴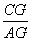 =
=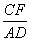 .
.
∵CG=AE,
∴AG=CE.
又∵在正方形ABCD中,AD=CB,
∴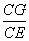 =
=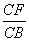 .
.
又∵∠GCF=∠ECB,
∴△CGF∽△CEB,
∴∠CGF=∠CEB,
∴ BE∥DF. 9分

 B.1 C.
B.1 C. D.2
D.2
 -
- = .
= .
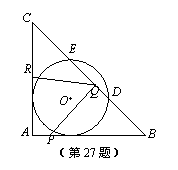 (3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合.
(3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B'与圆心O恰好重合. 心O(不写作法,保留作图痕迹);
心O(不写作法,保留作图痕迹);
 边形的内角和等于540°,则
边形的内角和等于540°,则 .
.