题目内容
12.解方程组或不等式(组):(1)$\left\{\begin{array}{l}{3x-5y=6}\\{x+4y=-15}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x-2(x-1)≤3}\\{\frac{2x+5}{3}>x}\end{array}\right.$.
分析 (1)用加减消元法或代入消元法求解;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:$\left\{\begin{array}{l}{3x-5y=6①}\\{x+4y=-15②}\end{array}\right.$,
由②得,x=-4y-15③,
把③代入①得,-12y-45-5y=6,解得y=-3.
把y=3代入③得,x=-3
故此方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-3}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x-2(x-1)≤3①}\\{\frac{2x+5}{3}>x②}\end{array}\right.$
由①得,x≥-1,
由②得,x<5,
故此方程组的解为:-1≤x<5.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
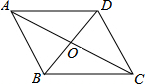 如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对.
如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对. 如图,在△AOD和△BOC中,AB与CD相交于点O,AO=BO,CO=DO,求证:△AOD≌△BOC.
如图,在△AOD和△BOC中,AB与CD相交于点O,AO=BO,CO=DO,求证:△AOD≌△BOC.