题目内容
20.下列说法正确的是( )| A. | 任何数的0次幂都等于1 | B. | (8×106)÷(2×109)=4×103 | ||
| C. | 所有等腰三角形都是锐角三角形 | D. | 三角形是边数最少的多边形 |
分析 根据0指数幂的定义可判断A;根据整式的除法:系数除以系数,同底数的幂相除,可判断B;等腰三角形可能为锐角三角形,可能为钝角三角形,也可能为直角三角形,可判断C;由多边形的定义可判断D.
解答 解:A、∵除0外,任何数的0次幂都等于1,故此选项错误;
B、∵(8×106)÷(2×109)=(8÷2)×106-9=4×10-3,故此选项错误;
C、∵当等腰三角形的顶角为钝角时,此等腰三角形为钝角三角形;当等腰三角形的顶角为锐角时,此等腰三角形为锐角三角形;当等腰三角形的顶角为直角时,此等腰三角形为直角三角形,故此选项错误;
D、由多边形的定义可判断D正确.
故选D.
点评 本题主要考查了多边形的定义,整式的除法,零指数幂,等腰三角形的性质,能理解性质和法则是解答此题的关键.

练习册系列答案
相关题目
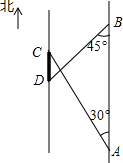 如图,一条南北走向的两岸互相平行.甲、乙二人分别站在河东岸的A、B处观察河西岸某景观建筑物.甲同学测得该建筑物一端C在A的北偏西30°方向,乙同学测得该建筑物另一端D在B的南偏西45°方向上.已知A、B点相距240米,河宽100米,求景观建筑物两端点C、D之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,一条南北走向的两岸互相平行.甲、乙二人分别站在河东岸的A、B处观察河西岸某景观建筑物.甲同学测得该建筑物一端C在A的北偏西30°方向,乙同学测得该建筑物另一端D在B的南偏西45°方向上.已知A、B点相距240米,河宽100米,求景观建筑物两端点C、D之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)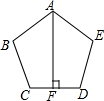 如图,正五边形ABCDE中,AF⊥CD,垂足为F
如图,正五边形ABCDE中,AF⊥CD,垂足为F