题目内容
5.点P(4,-3)到原点的距离是5.分析 过P作PM⊥x轴于M,求出PM=3,OM=4,根据勾股定理求出即可.
解答 解:过P作PM⊥x轴于M,如图:
∵P(4,-3),
∴PM=3,OM=4,
∴由勾股定理得:OP=$\sqrt{{4}^{2}+{3}^{2}}$=5.
故答案为:5.
点评 本题考查了坐标与图形性质,勾股定理的应用,注意:在直角三角形中,两条直角边的平方和等于斜边的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.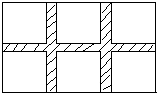 如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )
如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )
 如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )
如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )| A. | 100×80-100x-80×2x=7488 | B. | (100-2x)(80-x)=7488 | ||
| C. | (100-2x)(80-x)+2x2=7488 | D. | 100x+80×2x=512 |
20.下列说法正确的是( )
| A. | 任何数的0次幂都等于1 | B. | (8×106)÷(2×109)=4×103 | ||
| C. | 所有等腰三角形都是锐角三角形 | D. | 三角形是边数最少的多边形 |
15.某种商品的进价为a元,商店将价格提高50%后作为零售价销售,在销售旺季过后,商店又以7折的价格开展促销活动,这时,一件商品的促销价格为( )
| A. | a元 | B. | 0.7a元 | C. | 1.05a元 | D. | 0.93a元 |
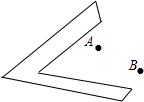 如图,在两相交公路有两村庄A、B,要修一个商店,要求到两村庄A、B的距离相等.到两公路的距离也相等.请你利用几何作图的方法,在下面的示意图中画出商店的位置.
如图,在两相交公路有两村庄A、B,要修一个商店,要求到两村庄A、B的距离相等.到两公路的距离也相等.请你利用几何作图的方法,在下面的示意图中画出商店的位置.