题目内容
20.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方形形状的无盖纸盒.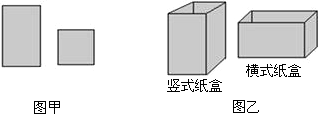
(1)现有正方形纸板150张,长方形纸板300张,设做竖式纸盒x个,横式纸盒y个,
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | 2y |
| 长方形纸板(张) | 4x | 3y |
(2)若有正方形纸板32张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完,已知70<a<75.则a的值是73.
分析 (1)①可根据每个竖式纸盒需1个正方形纸板和4个长方形纸板,每个横式纸盒需3个长方形纸板和2个正方形纸板来填空.
②生产竖式纸盒用的正方形纸板+生产横式纸盒用的正方形纸板=150张;生产竖式纸盒用的长方形纸板+生产横式纸盒用的长方形纸板=300张.由此得出符合条件的方案.
(2)设做竖式纸盒x个,横式纸盒y个,列出含有a的二元一次方程组,解方程组得出y关于a的等式,根据题中给出的a的取值范围便可求出y的取值范围,进而求出a的值.
解答 解:(1)①如表:
| 纸盒 纸板 | 竖式纸盒(个) | 横式纸盒(个) |
| x | y | |
| 正方形纸板(张) | x | 2y |
| 长方形纸板(张) | 4x | 3y |
解得:$\left\{\begin{array}{l}{x=30}\\{y=60}\end{array}\right.$.
答:生产竖式纸盒30个,横式纸盒60个;
(2)设做竖式纸盒x个,横式纸盒y个,
由题意得$\left\{\begin{array}{l}{x+2y=32}\\{4x+3y=a}\end{array}\right.$,
解得y=$\frac{128-a}{5}$,
∵70<a<75,则10.6<y<11.6,
∵y为整数,∴y取11,
当y=11时a=73.
故答案为:73.
点评 本题主要考查了二元一次方程组和一元一次不等式组的实际应用,解题关键是弄清题意,合适的等量关系,列出方程组,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.用下列各图表示数轴,正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
11.已知P1(x1,y1)、P2(x2,y2)、P3(x3,y3)是反比例函数y=$\frac{10}{x}$的图象上的三点,且x1<x2<0<x3,则y1、2、y3的大小关系是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y2<y3<y1 |
8. 如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
 如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
如图,已知点A在平面直角坐标系的位置,其坐标可能是( )| A. | (3,4) | B. | (-3,4) | C. | (3,-4) | D. | (-3,-4) |
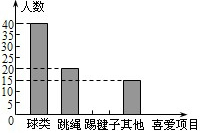 某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.
某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.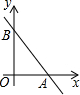 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,点P(m,0)为x轴上一点.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,点P(m,0)为x轴上一点.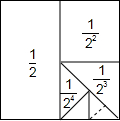 在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.
在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.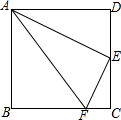 如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.
如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.