题目内容
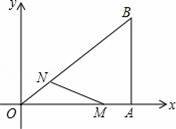
如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.

【考点】相似形综合题.
【专题】压轴题.
【分析】(1)由勾股定理求出OB,作NP⊥OA于P,则NP∥AB,得出△OPN∽△OAB,得出比例式
 ,求出OP、PN,即可得出点N的坐标;
,求出OP、PN,即可得出点N的坐标;
(2)由三角形的面积公式得出S是x的二次函数,即可得出S的最大值;
(3)分两种情况:①若∠OMN=90°,则MN∥AB,由平行线得出△OMN∽△OAB,得出比例式,即可求出x的值;
②若∠ONM=90°,则∠ONM=∠OAB,证出△OMN∽△OBA,得出比例式,求出x的值即可.
【解答】解:(1)根据题意得:MA=x,ON=1.25x,
在Rt△OAB中,由勾股定理得:OB=
 =
=
 =5,
=5,
作NP⊥OA于P,如图1所示:
则NP∥AB,
∴△OPN∽△OAB,
∴
 ,
,
即
 ,
,
解得:OP=x,PN=
 ,
,
∴点N的坐标是(x,
 );
);
(2)在△OMN中,OM=4﹣x,OM边上的高PN=
 ,
,
∴S=
 OM•PN=
OM•PN=
 (4﹣x)•
(4﹣x)•
 =﹣
=﹣
 x2+
x2+
 x,
x,
∴S与x之间的函数表达式为S=﹣
 x2+
x2+
 x(0<x<4),
x(0<x<4),
配方得:S=﹣
 (x﹣2)2+
(x﹣2)2+
 ,
,
∵﹣
 <0,
<0,
∴S有最大值,
当x=2时,S有最大值,最大值是
 ;
;
(3)存在某一时刻,使△OMN是直角三角形,理由如下:
分两种情况:①若∠OMN=90°,如图2所示:
则MN∥AB,
此时OM=4﹣x,ON=1.25x,
∵MN∥AB,
∴△OMN∽△OAB,
∴
 ,
,
即
 ,
,
解得:x=2;
②若∠ONM=90°,如图3所示:
则∠ONM=∠OAB,
此时OM=4﹣x,ON=1.25x,
∵∠ONM=∠OAB,∠MON=∠BOA,
∴△OMN∽△OBA,
∴
 ,
,
即
 ,
,
解得:x=
 ;
;
综上所述:x的值是2秒或
 秒.
秒.






【点评】本题是相似形综合题目,考查了相似三角形的判定与性质、勾股定理、坐标与图形特征、直角三角形的性质、三角形面积的计算、求二次函数的解析式以及最值等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,通过证明三角形相似才能得出结果.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

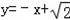
 的距离等于2的点共有( )
的距离等于2的点共有( )



 糖核酸(DNA)的分子直径为0.00000023cm,则这个数据用科学记数法表示为
糖核酸(DNA)的分子直径为0.00000023cm,则这个数据用科学记数法表示为