题目内容
2.先化简,再求值:$\frac{2-x}{{{x^2}-1}}-\frac{1}{1-x}$,其中x=$\sqrt{3}+1$.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{2-x}{(x+1)(x-1)}$+$\frac{x+1}{(x+1)(x-1)}$
=$\frac{2-x+x+1}{(x+1)(x-1)}$
=$\frac{3}{(x+1)(x-1)}$,
当x=$\sqrt{3}$+1时,
原式=$\frac{3}{(\sqrt{3}+1+1)(\sqrt{3}+1-1)}$
=$\frac{3}{\sqrt{3}(\sqrt{3}+2)}$
=$\frac{3}{3+2\sqrt{3}}$
=$\frac{3(3-2\sqrt{3})}{(3+2\sqrt{3})(3-2\sqrt{3})}$
=2$\sqrt{3}$-3.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
12.下列说法:
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.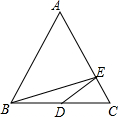 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | 3 | D. | $\sqrt{3}+1$ |
17.下列运算中错误的是( )
| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | $2\sqrt{2}+3\sqrt{2}=5\sqrt{2}$ | C. | $\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{{{(\sqrt{2}-\sqrt{3})}^2}}=\sqrt{2}-\sqrt{3}$ |