Question

如图，在四边形ABCD中，AD=4，CD=3，∠ABC=∠ACB=∠ADC=45°，则BD的长为

 

．

Answer 1

考点：全等三角形的判定与性质,勾股定理,等腰直角三角形

专题：计算题,压轴题

分析：根据等式的性质，可得∠BAD与∠CAD′的关系，根据SAS，可得△BAD与△CAD′的关系，根据全等三角形的性质，可得BD与CD′的关系，根据勾股定理，可得答案．

解答：解：作AD′⊥AD，AD′=AD，连接CD′，DD′，如图：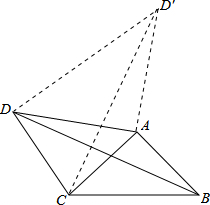
∵∠BAC+∠CAD=∠DAD′+∠CAD，
即∠BAD=∠CAD′，
在△BAD与△CAD′中，

BA=CA ∠BAD=∠CAD′ AD=AD′

，
∴△BAD≌△CAD′（SAS），
∴BD=CD′．
∠DAD′=90°
由勾股定理得DD′=

AD2+(AD′)2

=

32

=4

2

，
∠D′DA+∠ADC=90°
由勾股定理得CD′=

DC2+(DD′)2

=

9+32

=

41

，
∴BD=CD′=

41

，
故答案为：

41

．

点评：本题考查了全等三角形的判定与性质，利用了全等三角形的判定与性质，勾股定理，作出全等图形是解题关键．