题目内容
 在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从C点出发,以每秒1cm的速度向A点移动,同时点Q从C点出发以每秒2cm的速度向B点移动,那么需要
在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从C点出发,以每秒1cm的速度向A点移动,同时点Q从C点出发以每秒2cm的速度向B点移动,那么需要考点:一元二次方程的应用
专题:几何动点问题
分析:设t秒后△PCQ的面积等于5cm,分别表示出线段CP和线段CQ的长,再利用三角形的面积公式列出方程求解即可.
解答:解:设t秒后△PCQ的面积等于5cm,根据题意得:
CP=t,QC=2t,
则△PCQ的面积是:
CQ•CP=
×t×2t=5,
解得t1=
,t2=-
(舍去),
经过
秒后,△PCQ的面积等于5cm2.
故答案为:
.
CP=t,QC=2t,
则△PCQ的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
解得t1=
| 5 |
| 5 |
经过
| 5 |
故答案为:
| 5 |
点评:本题考查了一元二次方程的应用,解题的关键是根据题意找到等量关系并列出方程,用到的知识点是三角形的面积公式.

练习册系列答案
相关题目
 如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:
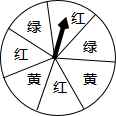 如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为
如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为
如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为