题目内容
如图，AB为⊙O的直径，AM和BN是它的两条切线，E为⊙O的半圆弧上一动点（不与A、B重合），过点E的直线分别交射线AM、BN于D、C两点，且CB=CE．（1）求证：CD为⊙O的切线；
（2）若AH=CH，求tan∠BAC的值．
考点：切线的判定与性质,相似三角形的判定与性质
专题：
分析：（1）连接OE．欲证CD为⊙O的切线，只需证明OE⊥CD即可；
（2）延长BE交AD于F，连OD、OC、AE，构建全等三角形：△AHF≌△CHB；求得BC=2AD，然后根据△AOD∽△BCO，求得AB=2
AD即可．
（2）延长BE交AD于F，连OD、OC、AE，构建全等三角形：△AHF≌△CHB；求得BC=2AD，然后根据△AOD∽△BCO，求得AB=2
| 2 |
解答：
解：（1）证明：连接OE．
∵OB=OE，
∴∠OBE=∠OEB．
∵BC=EC，
∴∠CBE=∠CEB，
∴∠OBC=∠OEC．
∵BC为⊙O的切线，
∴∠OEC=∠OBC=90°；
∵OE为半径，
∴CD为⊙O的切线；
（2）延长BE交AD于F，连OD、OC、AE．
∵DA、DC、为⊙O的切线，
∴DA=DE，
∴OD垂直平分AE，
∵OA=OB，
∴OD∥BE，
∴AD=DF，
即AF=2AD，
∵AD⊥AB，BC⊥AB，
∴AF∥BC，
在△AHF与△CHB中
，
∴△AHF≌△CHB（AAS）
∴AF=BC，
设AD=a，
∴BC=2a，
∵OD平分∠AOE，OC平分∠BOE，
∴∠AOD+∠BOC=90°，
∵∠AOD+∠ADO=90°，
∴∠ADO=∠BOC，
∵∠OAD=∠CBO=90°，
∴△AOD∽△BCO，
∴
=
，
∴
=
，
∴2AD2=OA2，
∴
AD=OA，
∴AB=2
AD，
∴tan∠BAC=
=
=
．
解：（1）证明：连接OE．
∵OB=OE，
∴∠OBE=∠OEB．
∵BC=EC，
∴∠CBE=∠CEB，
∴∠OBC=∠OEC．
∵BC为⊙O的切线，
∴∠OEC=∠OBC=90°；
∵OE为半径，
∴CD为⊙O的切线；
（2）延长BE交AD于F，连OD、OC、AE．
∵DA、DC、为⊙O的切线，
∴DA=DE，
∴OD垂直平分AE，
∵OA=OB，
∴OD∥BE，
∴AD=DF，
即AF=2AD，
∵AD⊥AB，BC⊥AB，
∴AF∥BC，
在△AHF与△CHB中
|
∴△AHF≌△CHB（AAS）
∴AF=BC，
设AD=a，
∴BC=2a，
∵OD平分∠AOE，OC平分∠BOE，
∴∠AOD+∠BOC=90°，
∵∠AOD+∠ADO=90°，
∴∠ADO=∠BOC，
∵∠OAD=∠CBO=90°，
∴△AOD∽△BCO，
∴
| AD |
| OA |
| OB |
| BC |
∴
| AD |
| OA |
| OA |
| 2AD |
∴2AD2=OA2，
∴
| 2 |
∴AB=2
| 2 |
∴tan∠BAC=
| BC |
| AB |
| 2AD | ||
2
|
| ||
| 2 |
点评：本题考查了圆的综合题：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角；直径所对的圆周角是直角，运用相似三角形的判定与性质进行计算．
练习册系列答案
相关题目
如图，在∠1、∠2、∠3、∠4、∠5、∠6中，同旁内角有（ ）| A、1对 | B、2对 | C、3对 | D、4对 |
如图，BD是△ABC的角平分线，点E，F分别在BC、AB上，且DE∥AB，EF∥AC．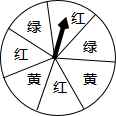
如图，一个转盘被分成7个相同的扇形，颜色分为红、黄、绿三种，指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，当作指向右边的扇形），则指针指向红色的概率为
如图，在四边形ABCD中，AD=4，CD=3，∠ABC=∠ACB=∠ADC=45°，则BD的长为