题目内容
已知,在△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F.
(1)若∠A=60°,求∠FDE的度数;
(2)若∠A=130°,求∠FDE的度数;
(3)你能猜想出∠FDE与∠A有什么数量关系吗?
(1)若∠A=60°,求∠FDE的度数;
(2)若∠A=130°,求∠FDE的度数;
(3)你能猜想出∠FDE与∠A有什么数量关系吗?
考点:三角形的内切圆与内心
专题:
分析:(1)连接IE,IF,根据切线的性质,可得出∠AEI和∠AFI等于90°,再由∠A=60°,从而得出∠EIF,根据同弧所对的圆周角是圆心角的一半,求得∠FDE.
(2)思路同(1);
(3)∠FDE=90°-
∠A.连结IE、IF,如图,根据切线的性质得到∠AEI=∠AFI=90°,利用四边形内角和得到∠A+∠EIF=180°,再由圆周角定理得∠EIF=2∠FDE,所以∠A+2∠EDF=180°,然后变形即可得到结论.
(2)思路同(1);
(3)∠FDE=90°-
| 1 |
| 2 |
解答:解:(1)连接IE,IF,
∵内切圆I和边BC、CA、AB分别相切于点D、E、F,
∴∠AEI=∠AFI=90°,
∵∠A=60°,
∴∠EIF=120°,
∴∠FDE=60°.
答:∠FDE的度数为60°;
(2)若∠A=130°,则∠FDE的度数=25°;
(3)∠FDE=90°-
∠A.理由如下:
连结IE、IF,如图,
∵内切圆I与边CA,AB分别相交于点E,F,
∴IE⊥AC,IF⊥AB,
∴∠AEI=∠AFI=90°,
∴∠A+∠EIF=180°,
∵∠EIF=2∠FDE,
∴∠A+2∠EDF=180°,
∴∠FDE=90°-
∠A.
∵内切圆I和边BC、CA、AB分别相切于点D、E、F,
∴∠AEI=∠AFI=90°,
∵∠A=60°,
∴∠EIF=120°,
∴∠FDE=60°.

答:∠FDE的度数为60°;
(2)若∠A=130°,则∠FDE的度数=25°;
(3)∠FDE=90°-
| 1 |
| 2 |
连结IE、IF,如图,
∵内切圆I与边CA,AB分别相交于点E,F,
∴IE⊥AC,IF⊥AB,
∴∠AEI=∠AFI=90°,
∴∠A+∠EIF=180°,
∵∠EIF=2∠FDE,
∴∠A+2∠EDF=180°,
∴∠FDE=90°-
| 1 |
| 2 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.熟练运用切线的性质.

练习册系列答案
相关题目
若分式
的值为0,则b的值为( )
| b2-1 |
| b2-2b-3 |
| A、1 | B、-1 | C、±1 | D、2 |
 如图,边长为a的正三角形的内切圆半径是( )
如图,边长为a的正三角形的内切圆半径是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知∠AOB=80°,∠AOC=40°,且OD是∠BOC的角平分线,则∠AOD的度数为( )
| A、20°或40° |
| B、20°或60° |
| C、20° |
| D、60° |
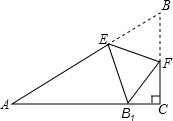 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6,点E、F分别在AB、BC上,沿EF将△EBF翻折,使顶点B的对应点B1落在AC上,若EB1⊥AC,则EF等于
如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6,点E、F分别在AB、BC上,沿EF将△EBF翻折,使顶点B的对应点B1落在AC上,若EB1⊥AC,则EF等于
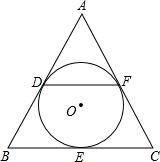 如图,△ABC的内切圆⊙O分别和AB,BC,CA切于点D,E,F,∠A=60°,BC=6,△ABC的周长为18,则DF的长为
如图,△ABC的内切圆⊙O分别和AB,BC,CA切于点D,E,F,∠A=60°,BC=6,△ABC的周长为18,则DF的长为