题目内容
已知∠AOB=80°,∠AOC=40°,且OD是∠BOC的角平分线,则∠AOD的度数为( )
| A、20°或40° |
| B、20°或60° |
| C、20° |
| D、60° |
考点:角平分线的定义
专题:
分析:分两种情况进行讨论:①OC在∠AOB外部,②OC在∠AOB内部,继而根据角平分线的定义分别运算即可得出答案.
解答:解:①当OC在∠AOB外部时,

∵∠AOB=80°,∠AOC=40°,
∴∠BOC=∠AOB+∠AOC=120°,
∵OD是∠BOC的角平分线,
∴∠BOD=
∠BOC=60°,
∴∠AOD=∠AOB-∠BOD=80°-60°=20°;
②当OC在∠AOB内部时,

∵∠AOB=80°,∠AOC=40°,
∴∠BOC=∠AOB-∠AOC=40°,
∵OD是∠BOC的角平分线,
∴∠BOD=
∠BOC=20°,
∴∠AOD=∠AOB-∠BOD=80°-20°=60°.
故选B.

∵∠AOB=80°,∠AOC=40°,
∴∠BOC=∠AOB+∠AOC=120°,
∵OD是∠BOC的角平分线,
∴∠BOD=
| 1 |
| 2 |
∴∠AOD=∠AOB-∠BOD=80°-60°=20°;
②当OC在∠AOB内部时,

∵∠AOB=80°,∠AOC=40°,
∴∠BOC=∠AOB-∠AOC=40°,
∵OD是∠BOC的角平分线,
∴∠BOD=
| 1 |
| 2 |
∴∠AOD=∠AOB-∠BOD=80°-20°=60°.
故选B.
点评:此题考查了角的运算,需要分类讨论OC的位置,有一定的难度,要求我们熟练掌握角平分线的定义与性质,注意不要漏解.

练习册系列答案
相关题目
 如图,坡角为1的斜坡上两树间的水平距离AC为2m,则两树间的坡面距离AB为( )
如图,坡角为1的斜坡上两树间的水平距离AC为2m,则两树间的坡面距离AB为( )| A、4m | ||||
B、
| ||||
C、
| ||||
D、4
|
一个正方体的表面展开图可以是下列图形中的( )
A、 |
B、 |
C、 |
D、 |
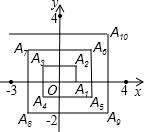 如图,在直角坐标系中,已知点A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、….则点A2015的坐标为
如图,在直角坐标系中,已知点A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、….则点A2015的坐标为