题目内容
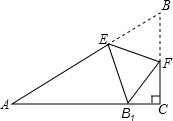 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6,点E、F分别在AB、BC上,沿EF将△EBF翻折,使顶点B的对应点B1落在AC上,若EB1⊥AC,则EF等于
如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6,点E、F分别在AB、BC上,沿EF将△EBF翻折,使顶点B的对应点B1落在AC上,若EB1⊥AC,则EF等于考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线;证明四边形BEB′F为菱形,此为解决该题的关键性结论;求出BE的长度,即可解决问题.
解答: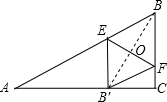 解:如图,连接BB′,交EF与点O;
解:如图,连接BB′,交EF与点O;
由题意得:BO=B′O,EF⊥BB′;
∵∠ACB=90°,且EB′⊥AC,
∴EB′∥BC,△EB′O∽△FBO,
∴
=
,
∴EO=FO,而EF⊥BB′,BO=B′O,
∴四边形BEB′F为菱形,
∴EB=EB′(设为λ),
则AE=6-λ;
∵∠A=30°,∠AB′E=90°,
∴6-λ=2λ,
解得:λ=2.
∵BE=BF,且∠ABC=90°-30°=60°,
∴△BEF为等边三角形,
∴EF=BE=2,
故答案为2.
 解:如图,连接BB′,交EF与点O;
解:如图,连接BB′,交EF与点O;由题意得:BO=B′O,EF⊥BB′;
∵∠ACB=90°,且EB′⊥AC,
∴EB′∥BC,△EB′O∽△FBO,
∴
| EO |
| FO |
| B′O |
| BO |
∴EO=FO,而EF⊥BB′,BO=B′O,
∴四边形BEB′F为菱形,
∴EB=EB′(设为λ),
则AE=6-λ;
∵∠A=30°,∠AB′E=90°,
∴6-λ=2λ,
解得:λ=2.
∵BE=BF,且∠ABC=90°-30°=60°,
∴△BEF为等边三角形,
∴EF=BE=2,
故答案为2.
点评:该题以直角三角形为载体,以翻折变换为方法,以考查菱形的判定、直角三角形的边角关系为核心构造而成;

练习册系列答案
相关题目
不论a为何值,分式
总有意义,则a的取值范围是( )
| 1 |
| x2-2x+a |
| A、a>1 | B、a≥1 |
| C、a<1 | D、a≤1 |
已知a,b,c为有理数,且a+b-c=0,abc<0,则
+
+
的值为( )
| b-c |
| |a| |
| a-c |
| |b| |
| a+b |
| |c| |
| A、-1 | B、1 | C、1或-1 | D、-3 |
 如图是一块长、宽、高分别是6cm,4cm和3cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长的平方是( )
如图是一块长、宽、高分别是6cm,4cm和3cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长的平方是( )| A、97 | B、109 | C、81 | D、85 |
在-2,-
,-3
,-π这四个数中,最大的数是( )
| 3 |
| 1 |
| 3 |
| A、-2 | ||
B、-
| ||
C、-3
| ||
| D、-π |
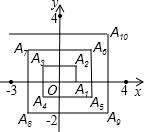 如图,在直角坐标系中,已知点A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、….则点A2015的坐标为
如图,在直角坐标系中,已知点A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、….则点A2015的坐标为