题目内容
19. 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=4cm.则图中阴影部分面积为$\frac{4}{3}$πcm2.(结果保留π)
如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=4cm.则图中阴影部分面积为$\frac{4}{3}$πcm2.(结果保留π)
分析 根据正方形的性质,可得边相等,角相等,根据扇形BAC与扇形CBD的弧交于点E,可得△BCE的形状,根据图形的割补,可得阴影的面积是扇形,根据扇形的面积公式,可得答案.
解答 解:∵四边形ABCD是正方形,
∴∠DCB=90°,DC=AB=4cm.
扇形BAC与扇形CBD的弧交于点E,
∴△BCE是等边三角形,∠ECB=60°,
∴∠DCE=∠DCB-∠ECB=30°.
根据图形的割补,可得阴影的面积是扇形DCE,
S扇形DCE=π×42×$\frac{30}{360}$=$\frac{4}{3}$πcm2.
故答案为:$\frac{4}{3}$πcm2.
点评 本题主要考查了正方形的性质,扇形的面积,灵活应用图形的割补是解题关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
9.计算(-3)-(-5)的结果等于( )
| A. | 8 | B. | -8 | C. | 2 | D. | -2 |
7.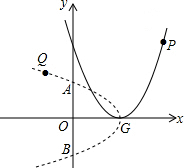 如图,点P为抛物线y=x2-4x+4上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.若点P的横坐标为4时,则Q点的坐标为( )
如图,点P为抛物线y=x2-4x+4上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.若点P的横坐标为4时,则Q点的坐标为( )
 如图,点P为抛物线y=x2-4x+4上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.若点P的横坐标为4时,则Q点的坐标为( )
如图,点P为抛物线y=x2-4x+4上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.若点P的横坐标为4时,则Q点的坐标为( )| A. | (-2,3) | B. | (-2,2$\sqrt{2}$) | C. | (-2,2) | D. | (1+$\frac{\sqrt{2}}{2}$,2) |
4.下列说法正确的是( )
| A. | 相等的两个角是对顶角 | |
| B. | 和等于180度的两个角互为邻补角 | |
| C. | 若两直线相交,则它们互相垂直 | |
| D. | 两条直线相交所形成的四个角都相等,则这两条直线互相垂直 |
9.2010年10月31日晚,中国2010上海世博会正式落下帷幕.据官网统计,累计参观人数超过73000 000人次,将73000 000用科学记数法表示应为( )
| A. | 0.73×108 | B. | 7.3×108 | C. | 7.3×107 | D. | 73×106 |
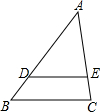 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若$\frac{AE}{AC}$=$\frac{3}{4}$,AD=9,则AB等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若$\frac{AE}{AC}$=$\frac{3}{4}$,AD=9,则AB等于( )