题目内容
15.计算1-2+3-4+5-…+(-1)n+1•n.(提示:分n为奇数和偶数两种情况来考虑)分析 两项一组,分n为奇数和偶数两种情况来考虑,求解即可.
解答 解:①n为奇数时,
1-2+3-4+5-…+(-1)n+1•n
=-1-1-1+…+n
=-1×$\frac{n-1}{2}$+n
=$\frac{n+1}{2}$;
②n为奇数时,
1-2+3-4+5-…+(-1)n+1•n
=-1-1-1-…-1
=-1×$\frac{n}{2}$
=-$\frac{n}{2}$.
点评 考查了有理数的加减混合运算,注意两项一组,以及分类思想的应用.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图,△ABC中,DF平分∠BDE,EF平分∠DEC,求证:AF平分∠BAC.
如图,△ABC中,DF平分∠BDE,EF平分∠DEC,求证:AF平分∠BAC.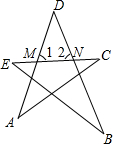 如图,图形ABCDE是五星形,∠1是△ACM的外角,那么∠1等于哪两个内角的和?∠2是△BEN的外角,那么∠2等于哪两个内角的和?由此可知∠A+∠B+∠C+∠D+∠E的和是多少度?
如图,图形ABCDE是五星形,∠1是△ACM的外角,那么∠1等于哪两个内角的和?∠2是△BEN的外角,那么∠2等于哪两个内角的和?由此可知∠A+∠B+∠C+∠D+∠E的和是多少度?