题目内容
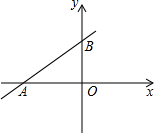
 如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-3,0),与反比例函数y=
如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-3,0),与反比例函数y=| k |
| x |
(1)求反比例函数的表达式和直线AB的表达式;
(2)若直线AB与y轴交于点C,求△COB的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)利用△AOB面积为9,求出m的值,即可求出反比例函数解析式,再利用A,B的坐标求出一次函数式.
(2)先求出OC,再利用△COB的面积为=
OC×3,求出△COB的面积.
(2)先求出OC,再利用△COB的面积为=
| 1 |
| 2 |
解答:解:(1)∵A点的坐标为(-3,0),
∴OA=3,
又∵点B(3,m)在第一象限,且△AOB面积为9,
∴
OA•m═9,即
×3m=9,解得m=6,
∴点B的坐标为(3,6),
将B(3,6)代入y=
中,得6=
,则k=18,
∴反比例函数为:y=
,
设直线AB的表达式为y=ax+b,则
解得
∴直线AB的表达式为y=x+3.
(2)在y=x+3中,令x=0,得y=3,
∴点C的坐标为 (0,3),
∴OC=3,
则△COB的面积为:
OC×3=
×3×3=
.
∴OA=3,
又∵点B(3,m)在第一象限,且△AOB面积为9,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴点B的坐标为(3,6),
将B(3,6)代入y=
| k |
| x |
| k |
| 3 |
∴反比例函数为:y=
| 18 |
| x |
设直线AB的表达式为y=ax+b,则
|
解得
|
∴直线AB的表达式为y=x+3.
(2)在y=x+3中,令x=0,得y=3,
∴点C的坐标为 (0,3),
∴OC=3,
则△COB的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
点评:本题主要考查了反比例函数与一次函数的交点问题,解题的关键是正确求出一次函数的解析式.

练习册系列答案
相关题目
 如图,已知直线l:y=
如图,已知直线l:y=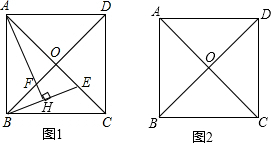 如图,已知正方形ABCD,AC、BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F.
如图,已知正方形ABCD,AC、BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F.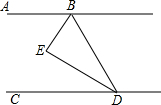 如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°. 为了改善小区环境,某小区决定在一块一边靠墙(墙长为25m)的空地上修建一个长方形绿化带ABCD.绿化带一面靠墙,另外三面用总长为40m的栅栏围住.
为了改善小区环境,某小区决定在一块一边靠墙(墙长为25m)的空地上修建一个长方形绿化带ABCD.绿化带一面靠墙,另外三面用总长为40m的栅栏围住.