题目内容
20.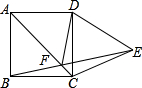 正方形ABCD的CD边长作等边△DCE,AC和BE相交于点F,连接DF.求∠AFD的度数.
正方形ABCD的CD边长作等边△DCE,AC和BE相交于点F,连接DF.求∠AFD的度数.
分析 根据等边三角形和正方形的性质证明△BCF≌△DCF,可得结论.
解答 解:在正方形ABCD和等边三角形DCE中,
∴CB=CD=CE,∠BCD=90°,∠DCE=60°,
∴△BCE是等腰三角形,且∠BCE=90°+60°=150°,
∴∠CBE=15°,
在△BCF和△DCF中,
∵$\left\{\begin{array}{l}{CB=CD}\\{∠ACB=∠ACD=45°}\\{CF=CF}\end{array}\right.$,
∴△BCF≌△DCF(SAS),
∴∠CBF=∠CDF=15°,
∴∠AFD=∠CDF+∠FCD=15°+45°=60°.
点评 本题考查了正方形的性质、等边三角形的性质、三角形全等的性质和判定,证明△BCE是等腰三角形,确定其底角的度数是关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
10.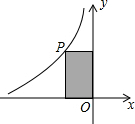 如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
 如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
 如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
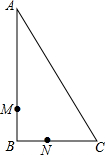 如图,在直角三角形ABC中,∠B=90°,点M、N分别在边BA,BC上,且BM=BN.
如图,在直角三角形ABC中,∠B=90°,点M、N分别在边BA,BC上,且BM=BN.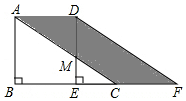 如图所示,将直角三角形ABC沿BC方向平移4cm,得到直角三角形DEF,连接AD,若AB=5cm,则图中阴影部分的面积为20cm2.
如图所示,将直角三角形ABC沿BC方向平移4cm,得到直角三角形DEF,连接AD,若AB=5cm,则图中阴影部分的面积为20cm2.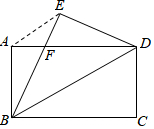 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.证明:
如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.证明: