题目内容
15.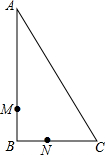 如图,在直角三角形ABC中,∠B=90°,点M、N分别在边BA,BC上,且BM=BN.
如图,在直角三角形ABC中,∠B=90°,点M、N分别在边BA,BC上,且BM=BN.(1)画出直角三角形ABC关于直线MN对称的三角形A′B′C′;
(2)如果AB=a,BC=b,BM=x,用a、b、x的代数式表示三角形AMA′的面积S1.
分析 (1)分别得出A,B,C点对称点,进而得出符合题意的图形;
(2)首先得出△AMA′是等腰直角三角形,进而利用三角形面积求法得出答案.
解答  解:(1)如图所示:△A′B′C′,即为所求;
解:(1)如图所示:△A′B′C′,即为所求;
(2)连接AA′、CC′
∵∠B=90°,BM=BN,
∴△BMN是等腰直角三角形,
∴△AMA′是等腰直角三角形,
∴S1=$\frac{1}{2}$(a-x)2=$\frac{1}{2}$a2-ax-$\frac{1}{2}$x2.
点评 此题主要考查了轴对称变换以及三角形面积求法,正确得出各对应点位置是解题关键.

练习册系列答案
相关题目
5.某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.[毛利润=(售价-进价)×销售量]
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
| A | B | |
| 进价(万元/套) | 1.5 | 1.2 |
| 售价(万元/套) | 1.65 | 1.4 |
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?

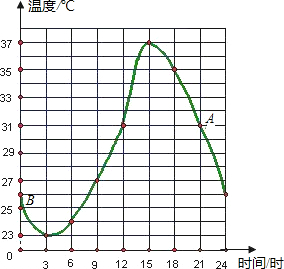 如图是某地某天温度变化的情况,根据图象回答问题:
如图是某地某天温度变化的情况,根据图象回答问题: 如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线BE交AD于点E,则DE=3.
如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线BE交AD于点E,则DE=3.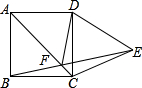 正方形ABCD的CD边长作等边△DCE,AC和BE相交于点F,连接DF.求∠AFD的度数.
正方形ABCD的CD边长作等边△DCE,AC和BE相交于点F,连接DF.求∠AFD的度数.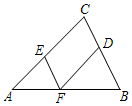 如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠EFD=∠C.
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠EFD=∠C. 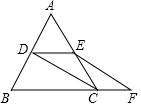 如图,等边三角形ABC中,D,E分别是AB,AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接DE,CD,EF.
如图,等边三角形ABC中,D,E分别是AB,AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接DE,CD,EF.