题目内容
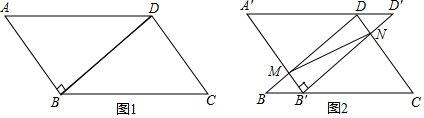
11．
如图，把△ABC向上平移4个单位长度，再向右平移3个单位长度，得到△A′B′C′．（1）在图中画出△A′B′C′，并写出点A′，B′，C′的坐标；
（2）连接A′、A、C′、C，求四边形AA′CC′的面积．
分析 （1）根据图形平移的性质画出△A′B′C′即可；根据各点在坐标系中的位置写出点A′、B′、C′的坐标；
（2）根据三角形的面积公式即可求出结果．
解答 解：（1）如图所示，△A′B′C′即为所求：
由图可知，A′（1，5），B′（0，2）、C′（4，2）；
（2）四边形A′ACC′的面积=S△A′AC′+S△ACC′=$\frac{1}{2}$×7×3+$\frac{1}{2}$×7×3=21．
点评 本题考查的是作图-平移变换，熟知图形平移不变性的性质是解答此题的关键．
练习册系列答案
相关题目
如图，AD为△ABC的高，BE为△ABC的角平分线，若∠EBA=34°，∠AEB=72°．
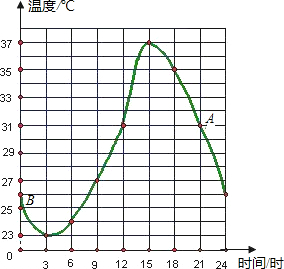如图是某地某天温度变化的情况，根据图象回答问题：
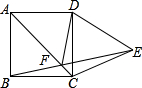正方形ABCD的CD边长作等边△DCE，AC和BE相交于点F，连接DF．求∠AFD的度数．
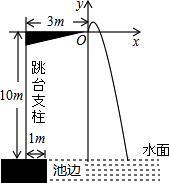如图，某运动员在2016年里约奥运会10米跳台跳水比赛时，估测身体（看成一点）在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x（图中标出的数据为已知条件），运动员在空中运动的最大高度离水面为10$\frac{2}{3}$米．