题目内容
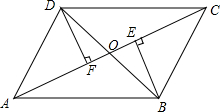 如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.
如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.(1)求证:△BOE≌△DOF;
(2)若OA=
| 1 |
| 2 |
考点:全等三角形的判定与性质
专题:
分析:(1)根据线段中点的定义可得OE=OF,根据垂直的定义可得∠OEB=∠OFD=90°,然后利用“角边角”证明△BOE和△DOF全等即可;
(2)根据全等三角形对应边相等可得OB=OD,然后求出OA=OB=OC=OD,再根据对角线相等且互相平分的四边形是矩形解答.
(2)根据全等三角形对应边相等可得OB=OD,然后求出OA=OB=OC=OD,再根据对角线相等且互相平分的四边形是矩形解答.
解答:(1)证明:∵点O是EF的中点,
∴OE=OF,
∵BE⊥AC,DF⊥AC,
∴∠OEB=∠OFD=90°,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA);
(2)解:四边形ABCD是矩形.
理由如下:∵△BOE≌△DOF,
∴OB=OD,
∵点O是AC的中点,
∴OA=OC,
∵OA=
BD,
∴OA=OB=OC=OD,
∴四边形ABCD是矩形.
∴OE=OF,
∵BE⊥AC,DF⊥AC,
∴∠OEB=∠OFD=90°,
在△BOE和△DOF中,
|
∴△BOE≌△DOF(ASA);
(2)解:四边形ABCD是矩形.
理由如下:∵△BOE≌△DOF,
∴OB=OD,
∵点O是AC的中点,
∴OA=OC,
∵OA=
| 1 |
| 2 |
∴OA=OB=OC=OD,
∴四边形ABCD是矩形.
点评:本题考查了全等三角形的判定与性质,矩形的判定,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
相关题目
若一个数的相反数是2,则这个数是( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)