题目内容
10．方程ax2+2x-1=0有两个相异的实数根，则a的取值范围是a＞-1且a≠0．分析 由关于x的一元二次方程ax2+2x-1=0有两个不相等的实数根，即可得判别式△＞0，继而可求得a的范围．
解答 解：∵关于x的一元二次方程ax2+2x-1=0有两个不相等的实数根，
∴△=b2-4ac=22-4×a×（-1）=4+4a＞0，
解得：a＞-1，
∵方程ax2+2x-1=0是一元二次方程，
∴a≠0，
∴a的范围是：a＞-1且a≠0．
故答案为：a＞-1且a≠0．
点评 此题考查了一元二次方程判别式的知识．此题比较简单，注意掌握一元二次方程有两个不相等的实数根，即可得△＞0．
练习册系列答案
相关题目
MF⊥NF于F，MF交AB于点E，NF交CD于点G，∠1=140°，∠2=50°，试判断AB和CD的位置关系，并说明理由．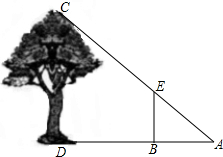
如图，某人在点A处测量树高，点A到树的距离AD为21米，将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面，此时，观察视线恰好经过标杆顶点E及树的顶点C，求树CD的高．
5．
如图，底面半径为1，高为$\sqrt{15}$的圆锥，侧面展开后成扇形，以扇形半径中点连线为边作矩形，其他两个顶点在弧上，则矩形的面积是（ ）
如图，底面半径为1，高为$\sqrt{15}$的圆锥，侧面展开后成扇形，以扇形半径中点连线为边作矩形，其他两个顶点在弧上，则矩形的面积是（ ）| A． | 4$\sqrt{5}$-4 | B． | 4$\sqrt{7}$-4 | C． | 8$\sqrt{2}$-4 | D． | 8-2$\sqrt{2}$ |
如图所示，长方形内有两个相邻的正方形，面积分别为3和5，那么阴影部分的面积为$\sqrt{15}$-3．