题目内容
4.某科研所需要960台机器,现有甲、乙两个工厂都想加工这批机器.已知甲工厂单独加工完成这批机器比乙工厂单独加工完成这批机器多用20天,且甲工厂、乙工厂每天加工机器台数之比为2:3,在加工过程中,科研所需每天付50元劳务费请工程师到厂进行技术指导,求:(1)甲、乙两个工厂每天各加工多少台机器?
(2)该科研所要选择既省时又省钱的加工厂加工,乙工厂通过商业途径得知甲工厂将向科研所上报加工费用为每天800元,请问:乙工厂向科研所上报加工费用每天最多为多少元时,才可以满足科研所要求,有望加工这批机器?
分析 (1)求的是工效,工作总量为960,一定是根据工作时间来列等量关系,本题的关键描述语是:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用20天.等量关系为:甲工厂单独加工完成这批产品天数-20=乙工厂单独加工完成这批产品的天数;
(2)设乙工厂报价为每天m元,根据乙工厂的总费用≤甲工厂的总费用,列出不等式即可求解.
解答 解:(1)设甲工厂每天加工2x件,则乙工厂每天加工3x件,由题意得:
$\frac{960}{2x}$-20=$\frac{960}{3x}$,
解得:x=8.
经检验,x=8是所列方程的根,
此时2x=16
3x=24.
答:甲工厂每天加工16台机器,乙工厂每天加工24台机器.
(2)由(1)可知加工960件产品,甲工厂要60天,乙工厂要40天.
所以甲工厂的加工总费用为60(800+50)=51000(元),
设乙工厂报价为每天m元,则乙工厂的加工总费用为40(m+50)元,
由题意得:40(m+50)≤51000,解得m≤1225.
答:乙工厂向科研所上报加工费用每天最多为1225元时,才可以满足科研所要求,有望加工这批机器.
点评 本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.注意利润率=利润成本×100%的应用.涉及到的公式:工作总量=工作效率×工作时间.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
15.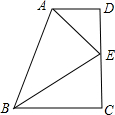 如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )
如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )
 如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )
如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )| A. | AE⊥BE | B. | CE=DE | C. | AD+DE=BE | D. | AB=AD+BC |
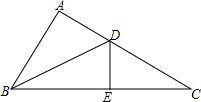 如图,△ADB≌△EDB,△BDE≌△CDE.B、E、C在一条直线上.
如图,△ADB≌△EDB,△BDE≌△CDE.B、E、C在一条直线上.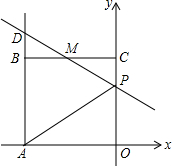 如图,已知正方形OABC的边长为4,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,n)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为4,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,n)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.