题目内容
1.袋中装有大小相同的2个红球、1个白球和1个绿球.(1)先从袋中摸出1个球后不放回,再摸出1个球,求两次摸到的球中有1个白球和1个红球的概率;
(2)先从袋中摸出1个球后放回,混合均匀后再摸出1个球.求两次摸到的球中有1个白球和1个红球的概率.(以上两题都要用画树状图或列表格求解)
分析 列表将所有等可能的结果列举出来,然后利用概率公式求解即可,注意(1)为不放回试验,(2)为放回试验.
解答 解:(1)列表得:
| 红 | 红 | 白 | 绿 | |
| 红 | 红红 | 红白 | 红绿 | |
| 红 | 红红 | 红白 | 红绿 | |
| 白 | 白红 | 白红 | 白绿 | |
| 绿 | 绿红 | 绿红 | 绿白 |
∴P(一红一白)=$\frac{4}{12}$=$\frac{1}{3}$;
(2)列表得:
| 红 | 红 | 白 | 绿 | |
| 红 | 红红 | 红红 | 红白 | 红绿 |
| 红 | 红红 | 红红 | 红白 | 红绿 |
| 白 | 白红 | 白红 | 白白 | 白绿 |
| 绿 | 绿红 | 绿红 | 绿白 | 绿绿 |
∴P(一红一白)=$\frac{4}{16}$=$\frac{1}{4}$;
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.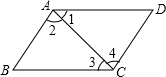 如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
 如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )| A. | ∠1=∠3 | B. | ∠2=∠4 | C. | ∠B=∠D | D. | ∠1+∠2+∠B=180° |
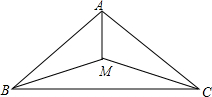 如图,在△ABC中,BM=MC,∠ABM=∠ACM,求证:AM平分∠BAC.
如图,在△ABC中,BM=MC,∠ABM=∠ACM,求证:AM平分∠BAC. 如图,D、E分别在△ABC的边上AC、AB上,请你添加一个条件∠ABC=∠ADE(答案不唯一)使得△ADE∽△ABC.
如图,D、E分别在△ABC的边上AC、AB上,请你添加一个条件∠ABC=∠ADE(答案不唯一)使得△ADE∽△ABC.