题目内容
两个大小相同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,点B,C,E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明,结论中不得含有未标识的字母)
(2)证明:DC⊥BE;
(3)如果点B,C,E不在一条直线上,(1)(2)中的结论是否成立?请画出两种不同类型的图形进行判断(不需写过程)

(1)请找出图2中的全等三角形,并给予证明(说明,结论中不得含有未标识的字母)
(2)证明:DC⊥BE;
(3)如果点B,C,E不在一条直线上,(1)(2)中的结论是否成立?请画出两种不同类型的图形进行判断(不需写过程)

考点:全等三角形的判定与性质,等腰直角三角形
专题:计算题
分析:(1)△ABE≌△ACD,理由为:由三角形ABC与三角形ADE都为等腰直角三角形,得到一对直角相等,两对边相等,利用等式的性质得到夹角相等,利用SAS即可得证;
(2)由(1)的结论,利用全等三角形对应角相等得到∠ACD=∠B=45°,进而得到∠ACB+∠ACD=90°,利用垂直的定义即可得证;
(3)如果点B,C,E不在一条直线上,(1)(2)中的结论仍然成立,如图所示.
(2)由(1)的结论,利用全等三角形对应角相等得到∠ACD=∠B=45°,进而得到∠ACB+∠ACD=90°,利用垂直的定义即可得证;
(3)如果点B,C,E不在一条直线上,(1)(2)中的结论仍然成立,如图所示.
解答:
解:(1)△ABE≌△ACD,理由为:
证明:∵△ABC与△ADE都为等腰直角三角形,
∴∠BAC=∠EAD=90°,AB=AC,AE=AD,
∴∠BAC+∠CAE=∠EAD+∠CAE,即∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS);
(2)∵△ABE≌△ACD,
∴∠ACD=∠B=45°,
∵∠B=∠ACB=45°,
∴∠DCB=∠ACD+∠ACB=90°,
∴DC⊥BE;
(3)如果点B,C,E不在一条直线上,(1)(2)中的结论依然成立,
如图所示:

证明:∵△ABC与△ADE都为等腰直角三角形,
∴∠BAC=∠EAD=90°,AB=AC,AE=AD,
∴∠BAC+∠CAE=∠EAD+∠CAE,即∠BAE=∠CAD,
在△ABE和△ACD中,
|
∴△ABE≌△ACD(SAS);
(2)∵△ABE≌△ACD,
∴∠ACD=∠B=45°,
∵∠B=∠ACB=45°,
∴∠DCB=∠ACD+∠ACB=90°,
∴DC⊥BE;
(3)如果点B,C,E不在一条直线上,(1)(2)中的结论依然成立,
如图所示:

点评:此题考查了全等三角形的判定与性质,以及等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,一个直角三角形ABC的斜边AB与量角器的零刻度线重合,点D对应56°,则∠BCD的度数为( )
如图,一个直角三角形ABC的斜边AB与量角器的零刻度线重合,点D对应56°,则∠BCD的度数为( )| A、28° | B、56° |
| C、62° | D、64° |
 在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是E、F.
在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是E、F.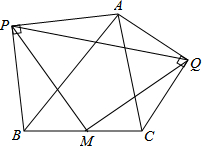 如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形.
如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形.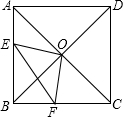 正方形ABCD中,AC,BD交于O,∠EOF=90°,已知AE=3,CF=4.则S△BEF为
正方形ABCD中,AC,BD交于O,∠EOF=90°,已知AE=3,CF=4.则S△BEF为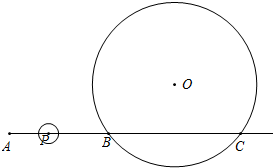 已知点C在射线AB上(点B在A、C之间),AB=12cm,BC=16cm,有一半径为10cm的⊙O过B、C两点,点P为射线AB上的一动点,且从点A出发,以1cm/秒的速度沿射线AB方向运动,设运动时间为t秒(t≥0),若以1cm为半径的⊙P与⊙O没有公共点,则t的取值范围为
已知点C在射线AB上(点B在A、C之间),AB=12cm,BC=16cm,有一半径为10cm的⊙O过B、C两点,点P为射线AB上的一动点,且从点A出发,以1cm/秒的速度沿射线AB方向运动,设运动时间为t秒(t≥0),若以1cm为半径的⊙P与⊙O没有公共点,则t的取值范围为