题目内容
 如图,一个直角三角形ABC的斜边AB与量角器的零刻度线重合,点D对应56°,则∠BCD的度数为( )
如图,一个直角三角形ABC的斜边AB与量角器的零刻度线重合,点D对应56°,则∠BCD的度数为( )| A、28° | B、56° |
| C、62° | D、64° |
考点:圆周角定理
专题:
分析:由∠ACB=90°,可得△ABC是以AB为直径的外接圆的内接三角形,然后由圆周角定理,求得∠ACD的度数,继而求得答案.
解答:
 解:∵∠ACB=90°,
解:∵∠ACB=90°,
∴△ABC是以AB为直径的外接圆的内接三角形,
∴∠ACD=
∠AOD=
×56°=28°,
∴∠BCD=90°-∠ACD=62°.
故选C.
 解:∵∠ACB=90°,
解:∵∠ACB=90°,∴△ABC是以AB为直径的外接圆的内接三角形,
∴∠ACD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BCD=90°-∠ACD=62°.
故选C.
点评:此题考查了圆周角定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
不等式组
的解集在数轴上表示为( )
|
A、 |
B、 |
C、 |
D、 |
 .下列结论中,正确的是( )
.下列结论中,正确的是( )
 时, y随x的增大而增大
时, y随x的增大而增大
 如图,是一个正方体的表面展开图,标注了字母“a”的面是正方体的正面,如果正方体相对两个面上的代数式的值相等,那么y-x的值为
如图,是一个正方体的表面展开图,标注了字母“a”的面是正方体的正面,如果正方体相对两个面上的代数式的值相等,那么y-x的值为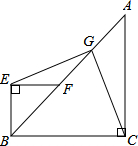 已知,如图,在△ABC中,∠ACB=90°,AC=BC,等腰直角三角形BEF的斜边在AB上,点G是AF的中点,联结EG,CG,求证:EG⊥CG.
已知,如图,在△ABC中,∠ACB=90°,AC=BC,等腰直角三角形BEF的斜边在AB上,点G是AF的中点,联结EG,CG,求证:EG⊥CG.
 如图,△ABC的边BC的垂直平分线与△ABC的外接圆相交于点D,若∠B=70°,∠C=50°,则
如图,△ABC的边BC的垂直平分线与△ABC的外接圆相交于点D,若∠B=70°,∠C=50°,则