Question

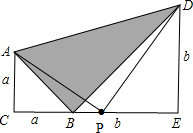
已知：两个等腰直角三角形（△ACB和△BED）边长分别为a和b（a＜b）如图放置在一起，连接AD．
（1）求△ABD的面积；
（2）如果有一个P点正好位于线段CE的中点，连接AP、DP得到△APD，求△APD的面积；
（3）（2）中的△APD的面积记为S₁，（1）中的△ABD的面积记为S₂，则S₁与S₂的大小关系是

 

．
A．S₁=S₂      B．S₁＜S₂       C．S₁＞S₂       D．无法确定．

Answer 1

考点：等腰直角三角形,整式的混合运算,三角形的面积

专题：

分析：（1）直接根据S_△ABD=

1

2

AB•BD进行计算即可；
（2）根据S_△APD=S_梯形ACDE-S_△ACP-S_△PED进行计算即可；
（3）分别求出△APD与△ABD的面积，利用作差法进行比较即可．

解答：解：（1）∵△ACB和△BED是等腰直角三角形，
∴△ABD是直角三角形，
AB=

2

a，BD=

2

b，
∴△ABD的面积=

1

2

AB•BD=

1

2

×

2

a×

2

b=ab，
（2）如图，

S_△APD=S_梯形ACED-S_△ACP-S_△PED
=

(a+b)2

2

-

a(a+b)

4

-

b(a+b)

4

，
=

1

2

a2+ab+

1

2

b2-

1

4

a2-

1

4

ab-

1

4

b²-

1

4

ab，
=

1

4

a2+

1

2

ab+

1

4

b²．
（3）∵S_△APD-S_△ABD=

1

4

（a+b）²-ab=

1

4

（a-b）²＞0，
∴S₁＞S₂．
故选：C．

点评：本题主要考查了梯形的判定、三角形的面积公式、梯形的面积公式及整式的混合运算．熟知梯形及三角形的面积公式是解答此题的关键．