题目内容
19．已知△ABC的各边长度分别为3cm、4cm、5cm，则连接各边中点的三角形周长为（ ）| A． | 2cm | B． | 7cm | C． | 5cm | D． | 6cm |
分析 根据三角形的中位线平行于第三边并且等于第三边的一半可得中点三角形的周长等于原三角形的周长的一半求解即可．
解答 解：∵△ABC的周长=3+4+5=12cm，
∴连接各边中点的三角形周长=$\frac{1}{2}$×12=6cm．
故选D．
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半，熟记定理并判断出中点三角形的周长等于原三角形的周长的一半是解题的关键．
练习册系列答案
小学课时特训系列答案
相关题目
7．
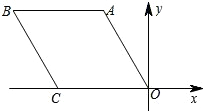如图，菱形OABC在平面直角坐标系中的位置如图所示，若OA=2，∠AOC=60°，则B点的坐标是（ ）
如图，菱形OABC在平面直角坐标系中的位置如图所示，若OA=2，∠AOC=60°，则B点的坐标是（ ）| A． | （3，$\sqrt{3}$） | B． | （1，$\sqrt{3}$） | C． | （-1，$\sqrt{3}$） | D． | （-3，$\sqrt{3}$） |
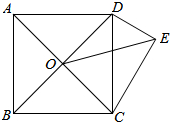如图，ABCD为正方形，O为AC、BD的交点，△DCE为Rt△，∠CED=90°，∠DCE=30°，若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$，则正方形的面积为（ ）
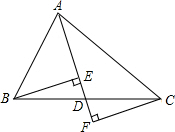如图，在△ABC中，点D是BC边的中点，分别过点B、C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F，求证：DE=DF．