题目内容
12. 如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F,BD=DC,求证:AD⊥BC.
如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F,BD=DC,求证:AD⊥BC.
分析 根据角平分线的性质得到DE=DF,证明Rt△DEB≌Rt△DFC,得到∠B=∠C,根据等腰三角形的性质证明结论.
解答 证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△DEB和Rt△DFC中,
$\left\{\begin{array}{l}{DE=DF}\\{BD=CD}\end{array}\right.$,
∴Rt△DEB≌Rt△DFC,
∴∠B=∠C,
∴AB=AC,又AD平分∠BAC,
∴AD⊥BC.
点评 本题考查的是角平分线的性质和全等三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
20.下列各式计算正确的是( )
| A. | $\frac{1}{a+b}$÷(a+b)=1 | B. | 2ab•$\frac{3{b}^{2}}{2a}$=3b2 | ||
| C. | $\frac{{a}^{2}-9}{a}$÷$\frac{{a}^{2}+3a}{{a}^{2}}$=a-3 | D. | $\frac{{x}^{2}+8x+16}{x-4}$$•\frac{1}{x+4}$=1 |
17.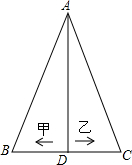 如图是三角形的土地ABC,AB=AC,△ABC中间一条小路AD,AD平分∠BAC,交BC于点D.甲、乙两人从点D出发,分别步行到B、C两点,则甲、乙两人步行的距离( )
如图是三角形的土地ABC,AB=AC,△ABC中间一条小路AD,AD平分∠BAC,交BC于点D.甲、乙两人从点D出发,分别步行到B、C两点,则甲、乙两人步行的距离( )
 如图是三角形的土地ABC,AB=AC,△ABC中间一条小路AD,AD平分∠BAC,交BC于点D.甲、乙两人从点D出发,分别步行到B、C两点,则甲、乙两人步行的距离( )
如图是三角形的土地ABC,AB=AC,△ABC中间一条小路AD,AD平分∠BAC,交BC于点D.甲、乙两人从点D出发,分别步行到B、C两点,则甲、乙两人步行的距离( )| A. | 甲步行的路程远 | B. | 乙步行的路程远 | C. | 一样远 | D. | 无法比较 |
 如图,已知AB=AC=10cm,AD=BD,ED⊥AB于点D,若BC=8cm,则△BEC的周长为18cm.
如图,已知AB=AC=10cm,AD=BD,ED⊥AB于点D,若BC=8cm,则△BEC的周长为18cm.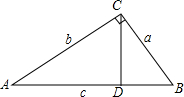 如图,△ABC中,∠ACB=90°,AB=c,BC=a,AC=b,且(c-$\sqrt{8}$)2+|$\sqrt{2}$-a|=0.
如图,△ABC中,∠ACB=90°,AB=c,BC=a,AC=b,且(c-$\sqrt{8}$)2+|$\sqrt{2}$-a|=0.