题目内容
5.下列各式中,计算正确的是( )| A. | x(2x-1)=2x2-1 | B. | $\frac{x+3}{{x}^{2}-9}$=$\frac{1}{x-3}$ | C. | (a+2)2=a2+4 | D. | (x+2)(x-3)=x2+x-6 |
分析 A、原式利用单项式乘以多项式法则计算得到结果,即可作出判断;
B、原式约分得到最简结果,即可作出判断;
C、原式利用完全平方公式化简得到结果,即可作出判断;
D、原式利用多项式乘以多项式法则计算得到结果,即可作出判断.
解答 解:A、原式=2x2-x,错误;
B、原式=$\frac{x+3}{(x+3)(x-3)}$=$\frac{1}{x-3}$,正确;
C、原式=a2+4a+4,错误;
D、原式=x2-x-6,错误,
故选B
点评 此题考查了完全平方公式,单项式乘多项式,多项式乘多项式,以及约分,熟练掌握公式及法则是解本题的关键.

练习册系列答案
相关题目
7.下列计算,正确的是( )
| A. | a2•a2=2a2 | B. | a2+a2=a4 | C. | (-a2)2=a4 | D. | (a+1)2=a2+1 |
 如图是由四个大小完全相同的正方体组成的几何体,那么它的俯视图是( )
如图是由四个大小完全相同的正方体组成的几何体,那么它的俯视图是( )



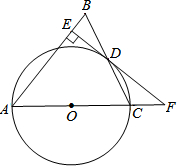 如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.