题目内容
 如图,正方形ABCD边长为4,E、F分别是BC、CD上的两个动点(点E不与点B重合),∠AEF=90°,连接AF.
如图,正方形ABCD边长为4,E、F分别是BC、CD上的两个动点(点E不与点B重合),∠AEF=90°,连接AF.(1)试找出图中一定相似的三角形,简要证明过程;
(2)试找出图中不一定相似的三角形,并确定当其相似时点E所在的位置,简写推理过程;
(3)试找出图中一定不相似的三角形,简要说明理由.
考点:相似三角形的判定,正方形的性质
专题:
分析:(1)由四边形ABCD是正方形,可得∠B=∠C=90°,又由∠AEF=90°,即可证得∠BAE=∠CEF,则可得△ABE∽△ECF;
(2)由△ABE∽△ECF,可得AB:EC=AE:EF,即可知当BE=CE,△ABE∽△AEF,则可得△AEF∽△ECF.
(3)△ABE不相似于△ADF,△ECF不相似于△ADF,△AEF不相似于△ADF,各边不成比例.
(2)由△ABE∽△ECF,可得AB:EC=AE:EF,即可知当BE=CE,△ABE∽△AEF,则可得△AEF∽△ECF.
(3)△ABE不相似于△ADF,△ECF不相似于△ADF,△AEF不相似于△ADF,各边不成比例.
解答:解:(1)△ABE∽△ECF.
理由:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵∠AEF=90°,
∴∠AEB+∠CEF=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF;
(2)当BE=CE=2时,△ABE∽△AEF或△AEF∽△ECF.
理由:∵△ABE∽△ECF,
∴AB:EC=AE:EF,
∵BE=CE,
∴AB:AE=BE:EF,
∵∠B=∠AEF=90°,
∴△ABE∽△AEF,
同理:△AEF∽△ECF.
∴当BE=CE=2,即E是BC中点时,△ABE∽△AEF或△AEF∽△ECF.
(3)△ABE不相似于△ADF,△ECF不相似于△ADF,△AEF不相似于△ADF.
∵∠AEF=90°,
∴AF>AE,
∵∠B=∠D=90°,AB=AD,
∴AB:AD≠AE:AF,
∴△ABE不相似于△ADF.
同理:△ECF不相似于△ADF,△AEF不相似于△ADF.
理由:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵∠AEF=90°,
∴∠AEB+∠CEF=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF;
(2)当BE=CE=2时,△ABE∽△AEF或△AEF∽△ECF.
理由:∵△ABE∽△ECF,
∴AB:EC=AE:EF,
∵BE=CE,
∴AB:AE=BE:EF,
∵∠B=∠AEF=90°,
∴△ABE∽△AEF,
同理:△AEF∽△ECF.
∴当BE=CE=2,即E是BC中点时,△ABE∽△AEF或△AEF∽△ECF.
(3)△ABE不相似于△ADF,△ECF不相似于△ADF,△AEF不相似于△ADF.
∵∠AEF=90°,
∴AF>AE,
∵∠B=∠D=90°,AB=AD,
∴AB:AD≠AE:AF,
∴△ABE不相似于△ADF.
同理:△ECF不相似于△ADF,△AEF不相似于△ADF.
点评:此题考查了相似三角形的判定与正方形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
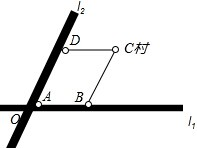 如图所示,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D,已知AD=AB=6km,CD=CB=5km,村庄C到公路l1的距离为4km,则村庄C到公路l2的距离是
如图所示,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D,已知AD=AB=6km,CD=CB=5km,村庄C到公路l1的距离为4km,则村庄C到公路l2的距离是 如图,AB是⊙O的直径,AC是弦,过
如图,AB是⊙O的直径,AC是弦,过
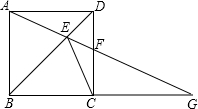 如图,正方形ABCD中,点E是对角线BD上的一点,连结AE并延长,交CD于点F,交BC的延长线于点G,连结CE.
如图,正方形ABCD中,点E是对角线BD上的一点,连结AE并延长,交CD于点F,交BC的延长线于点G,连结CE.