题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象开口向上,对称轴x<-1,与y轴交点纵坐标在0和-1之间,图象过(2,4)点,有下列结论:(1)abc>0;(2)2a-b>0;(3)20a<(4a+b)2;(4)0<a<
;其中正确结论有哪些,并说明理由.
| 5 |
| 8 |
考点:二次函数图象与系数的关系
专题:
分析:根据题意作出草图,由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及点(2,4)情况进行推理,进而对所得结论进行判断.
解答: 解:(1)由开口向上,则a>0,对称轴在y轴的左侧,a、b同号,则ab>0.
解:(1)由开口向上,则a>0,对称轴在y轴的左侧,a、b同号,则ab>0.
抛物线与y轴交于负半轴,则c<0,
所以 abc<0.
故(1)错误;
(2)抛物线开口方向向上,则a>0,对称轴x=-
<-1,故b>2a,即2a-b<0.
故(2)错误;
(3)∵当x=2时,y=4,
∴4=4a+2b+c,
∴(4a+2b)2=(c-4)2
∵c在0和-1之间,
∴16<(c-4)2<25
∵b<2a,
∴8a<4-c,
∵c在0和-1之间,
∴8a<5,
∴a<
,
∴20a<
,
∴20a<(4a+b)2
故(3)正确;
(4)由(1)(3)可知0<a<
,
故(4)正确.
 解:(1)由开口向上,则a>0,对称轴在y轴的左侧,a、b同号,则ab>0.
解:(1)由开口向上,则a>0,对称轴在y轴的左侧,a、b同号,则ab>0.抛物线与y轴交于负半轴,则c<0,
所以 abc<0.
故(1)错误;
(2)抛物线开口方向向上,则a>0,对称轴x=-
| b |
| 2a |
故(2)错误;
(3)∵当x=2时,y=4,
∴4=4a+2b+c,
∴(4a+2b)2=(c-4)2
∵c在0和-1之间,
∴16<(c-4)2<25
∵b<2a,
∴8a<4-c,
∵c在0和-1之间,
∴8a<5,
∴a<
| 5 |
| 8 |
∴20a<
| 25 |
| 2 |
∴20a<(4a+b)2
故(3)正确;
(4)由(1)(3)可知0<a<
| 5 |
| 8 |
故(4)正确.
点评:本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
相关题目
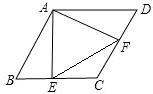 如图,在菱形ABCD中,E、F分别是CB、CD上的点,BE=DF,连接E、F,若E、F分别是CB、CD的中点,△AEF为等边三角形.求证:AE垂直平分BC.
如图,在菱形ABCD中,E、F分别是CB、CD上的点,BE=DF,连接E、F,若E、F分别是CB、CD的中点,△AEF为等边三角形.求证:AE垂直平分BC.