题目内容
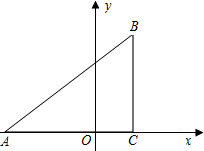 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),B(1,3).
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),B(1,3).(1)求线段AC和BC的长;
(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得△APQ与△ADB相似?如果存在,请求出m的值;如果不存在,请说明理由.
考点:相似形综合题
专题:综合题
分析:(1)由点A、B、C的坐标就可求出线段AC和BC的长.
(2)运用相似三角形的性质就可求出点D的坐标.
(3)由于△APQ与△ADB已有一组公共角相等,只需分△APQ∽△ABD和△APQ∽△ADB两种情况讨论,然后运用相似三角形的性质建立关于m的方程,就可解决问题.
(2)运用相似三角形的性质就可求出点D的坐标.
(3)由于△APQ与△ADB已有一组公共角相等,只需分△APQ∽△ABD和△APQ∽△ADB两种情况讨论,然后运用相似三角形的性质建立关于m的方程,就可解决问题.
解答:解:(1)∵点A、B、C的坐标分别为A(-3,0)、B(1,3)、C(1,0),
∴∠ACB=90°,AC=1+3=4,BC=3.
∴线段AC和BC的长分别为4,3.
(2)若△ADB与△ABC相似(不包括全等),则有∠ABD=90°,如图1,
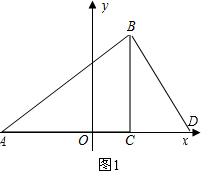
此时
=
,即AB2=AC•AD.
∵∠ACB=90°,AC=4,BC=3,
∴AB=5,
∴25=4AD,
∴AD=
,
∴OD=AD-AO=
-3=
,
∴点D的坐标为(
,0).
(3)∵AP=DQ=m,∴AQ=AD-QD=
-m.
①若△APQ∽△ABD,如图2,
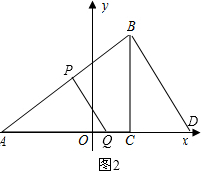
则有
=
,
∴AP•AD=AB•AQ,
∴
m=5(
-m),
解得;m=
.
②若△APQ∽△ADB,如图3,
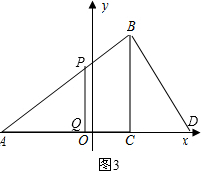
则有
=
,
∴AP•AB=AD•AQ,
∴5m=
(
-m),
解得:m=
.
综上所述:符合要求的m的值为
或
.
∴∠ACB=90°,AC=1+3=4,BC=3.
∴线段AC和BC的长分别为4,3.
(2)若△ADB与△ABC相似(不包括全等),则有∠ABD=90°,如图1,

此时
| AB |
| AC |
| AD |
| AB |
∵∠ACB=90°,AC=4,BC=3,
∴AB=5,
∴25=4AD,
∴AD=
| 25 |
| 4 |
∴OD=AD-AO=
| 25 |
| 4 |
| 13 |
| 4 |
∴点D的坐标为(
| 13 |
| 4 |
(3)∵AP=DQ=m,∴AQ=AD-QD=
| 25 |
| 4 |
①若△APQ∽△ABD,如图2,

则有
| AP |
| AB |
| AQ |
| AD |
∴AP•AD=AB•AQ,
∴
| 25 |
| 4 |
| 25 |
| 4 |
解得;m=
| 25 |
| 9 |
②若△APQ∽△ADB,如图3,

则有
| AP |
| AD |
| AQ |
| AB |
∴AP•AB=AD•AQ,
∴5m=
| 25 |
| 4 |
| 25 |
| 4 |
解得:m=
| 125 |
| 36 |
综上所述:符合要求的m的值为
| 25 |
| 9 |
| 125 |
| 36 |
点评:本题考查了相似三角形的判定与性质、勾股定理等知识,考查了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
圆内接四边形ABCD中,∠A:∠B:∠C:∠D可以是( )
| A、5:2:3:4 |
| B、5:3:2:4 |
| C、2:4:3:5 |
| D、4:2:5:3 |
将抛物线y=-
x2+2x-5配成y=a(x-h)2+k的形式为( )
| 1 |
| 3 |
A、y=-
| ||
B、y=-
| ||
C、y=-
| ||
D、y=-
|
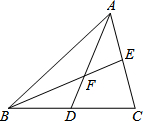 如图,△ABC的中线AD、BE相交于点F.△ABF与四边形CEFD的面积有怎样的数量关系?为什么?
如图,△ABC的中线AD、BE相交于点F.△ABF与四边形CEFD的面积有怎样的数量关系?为什么?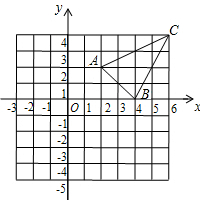 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(6,4)以原点为位似中心,将△ABC缩小,位似比为1:2,则线段AC中点P变换后对应点的坐标为
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(6,4)以原点为位似中心,将△ABC缩小,位似比为1:2,则线段AC中点P变换后对应点的坐标为 如图,已知∠AOB,
如图,已知∠AOB, 如图,四边形ABCD中,∠A=90°,∠C=90°,EF分别是BD、AC的中点,请你说明EF与AC的位置关系.
如图,四边形ABCD中,∠A=90°,∠C=90°,EF分别是BD、AC的中点,请你说明EF与AC的位置关系.