题目内容
 如图,四边形ABCD中,∠A=90°,∠C=90°,EF分别是BD、AC的中点,请你说明EF与AC的位置关系.
如图,四边形ABCD中,∠A=90°,∠C=90°,EF分别是BD、AC的中点,请你说明EF与AC的位置关系.考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:
分析:连接AE、CE,根据直角三角形斜边上中线性质求出AE=CE,根据等腰三角形的性质得出即可.
解答:解: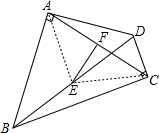
EF⊥AC,
理由是:连接AE、CE,
∵∠BAD=∠BCD=90°,E为BD中点,
∴AE=
BD,CE=
BD,
∴AE=CE,
∵F为AC中点,
∴EF⊥AC.

EF⊥AC,
理由是:连接AE、CE,
∵∠BAD=∠BCD=90°,E为BD中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=CE,
∵F为AC中点,
∴EF⊥AC.
点评:本题考查了直角三角形斜边上中线性质,等腰三角形的性质的应用,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
下列事件是必然事件的是( )
| A、抛掷一枚硬币100次,有50次正面朝上 |
| B、面积相等的两个三角形全等 |
| C、a是实数,|a|>0 |
| D、方程x2-2x-1=0必有实数根 |
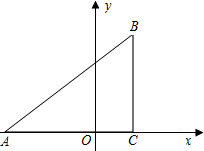 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),B(1,3).
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),B(1,3).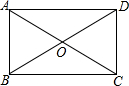 如图,在矩形ABCD中,对角线AC、BD相交于O,AB=OA=3,则BC=
如图,在矩形ABCD中,对角线AC、BD相交于O,AB=OA=3,则BC= 如图,在⊙O中,弦AB所对的优弧为圆的
如图,在⊙O中,弦AB所对的优弧为圆的 如图,AB=DB,∠1=∠2,请你添加一个适当的条件,使△ABC≌△DBE,请问添加下面哪个条件不能判断△ABC≌△DBE的有
如图,AB=DB,∠1=∠2,请你添加一个适当的条件,使△ABC≌△DBE,请问添加下面哪个条件不能判断△ABC≌△DBE的有