题目内容
将抛物线y=-
x2+2x-5配成y=a(x-h)2+k的形式为( )
| 1 |
| 3 |
A、y=-
| ||
B、y=-
| ||
C、y=-
| ||
D、y=-
|
考点:二次函数的三种形式
专题:
分析:利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑成完全平方式,即可把一般式转化为顶点式;
解答:解:y=-
x2+2x-5
=-
(x2-6x+9)-5+3
=-
(x-3)2-2.
故选:C.
| 1 |
| 3 |
=-
| 1 |
| 3 |
=-
| 1 |
| 3 |
故选:C.
点评:本题考查了二次函数的三种形式、配方法的应用.二次函数的解析式有三种形式:
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
(2)顶点式:y=a(x-h)2+k;
(3)交点式(与x轴):y=a(x-x1)(x-x2).
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
(2)顶点式:y=a(x-h)2+k;
(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
相关题目
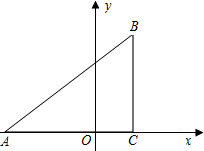 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),B(1,3).
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),B(1,3).
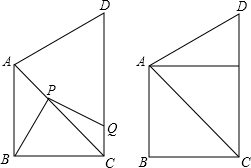 如图,在四边形ABCD中,AB=BC=1,∠ABC=90°,且AB∥CD,将一把三角尺的直角顶点P放在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,探究:
如图,在四边形ABCD中,AB=BC=1,∠ABC=90°,且AB∥CD,将一把三角尺的直角顶点P放在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,探究: