题目内容
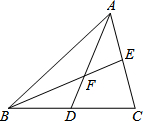如图，△ABC的中线AD、BE相交于点F．△ABF与四边形CEFD的面积有怎样的数量关系？为什么？考点：三角形的面积
专题：
分析：根据等底等高的三角形的面积相等可知三角形的中线把三角形分成面积相等的两个三角形，然后表示出S△ABE=S△ACD=
S△ABC，再表示出S△ABF与S四边形CEFD，即可得解．
| 1 |
| 2 |
解答：解：∵AD、BE是△ABC的中线，
∴S△ABE=S△ACD=
S△ABC，
∵S△ABF=S△ABE-S△AEF，S四边形CEFD=S△ACD-S△AEF，
∴S△ABF=S四边形CEFD，
即，△ABF与四边形CEFD的面积相等．
∴S△ABE=S△ACD=
| 1 |
| 2 |
∵S△ABF=S△ABE-S△AEF，S四边形CEFD=S△ACD-S△AEF，
∴S△ABF=S四边形CEFD，
即，△ABF与四边形CEFD的面积相等．
点评：本题考查了三角形的面积，熟记三角形的中线把三角形分成面积相等的两个三角形是解题的关键．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
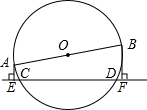如图，AB是⊙O直径，CD是弦．若AB=85，CD=75，那么A、B两点到直线CD的距离之和为
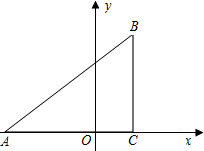已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A，C的坐标分别为A（-3，0），C（1，0），B（1，3）．
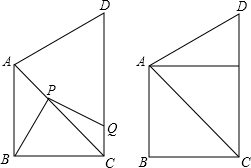如图，在四边形ABCD中，AB=BC=1，∠ABC=90°，且AB∥CD，将一把三角尺的直角顶点P放在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q，探究：下列事件是必然事件的是（ ）
| A、抛掷一枚硬币100次，有50次正面朝上 |
| B、面积相等的两个三角形全等 |
| C、a是实数，|a|＞0 |
| D、方程x2-2x-1=0必有实数根 |