题目内容
 如图,在等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.求证:△APQ是等边三角形.
如图,在等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.求证:△APQ是等边三角形.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:易证AB=AC,∠BAC=60°,即可证明△ABP≌△ACQ,可得∠BAP=∠CAQ,AP=AQ,即可求得∠PAQ=60°,即可解题.
解答:证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
在△ABP和△ACQ中,
,
∴△ABP≌△ACQ,(SAS)
∴∠BAP=∠CAQ,AP=AQ,
∵∠BAP+∠CAP=60°,
∴∠PAQ=∠CAQ+∠CAQ=60°,
∴△APQ是等边三角形.
∴AB=AC,∠BAC=60°,
在△ABP和△ACQ中,
|
∴△ABP≌△ACQ,(SAS)
∴∠BAP=∠CAQ,AP=AQ,
∵∠BAP+∠CAP=60°,
∴∠PAQ=∠CAQ+∠CAQ=60°,
∴△APQ是等边三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了正三角形的判定,本题中求证△ABP≌△ACQ是解题的关键.

练习册系列答案
相关题目
甲乙两地相距约12 900m,把12 900m用科学记数法可以记为( )
| A、129×102m |
| B、12.9×103m |
| C、1.29×104m |
| D、0.129×105m |
若|x-
|+|2y+1|=0,则x2+y2的值是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 如图.在△ABC中,∠C=90°,AC=8,AB=10,点P在线段AC上运动,若圆O的半径是y,AP=x,且⊙0的圆心在线段BP上,圆O与AB,AC都相切.请求出y与x的函数关系式.
如图.在△ABC中,∠C=90°,AC=8,AB=10,点P在线段AC上运动,若圆O的半径是y,AP=x,且⊙0的圆心在线段BP上,圆O与AB,AC都相切.请求出y与x的函数关系式.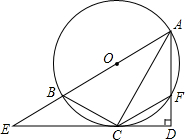 如图,Rt△ADE中,∠D=90°,点O为斜边上一点,以AB为直径的⊙O交ED于点C,连接CA、CB、CF,
如图,Rt△ADE中,∠D=90°,点O为斜边上一点,以AB为直径的⊙O交ED于点C,连接CA、CB、CF,
 如图,△ABC的内心为点I,外心为点O,且∠BIC=115°,求∠BOC的度数.
如图,△ABC的内心为点I,外心为点O,且∠BIC=115°,求∠BOC的度数.