题目内容
16.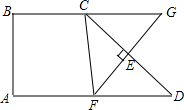 如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=BC,∠D=45°,CD的垂直平分线交CD于E,交AD于F,交BC的延长线于G,若AD=a.
如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=BC,∠D=45°,CD的垂直平分线交CD于E,交AD于F,交BC的延长线于G,若AD=a.(1)求证:四边形ABCF是正方形;
(2)求BG的长.
分析 (1)先根据∠B=∠A=∠AFC=90°,判定四边形ABCF是矩形,再根据AB=BC,即可得到四边形ABCF是正方形;
(2)先判定△CEG≌△DEF(AAS),得出CG=FD,再根据正方形ABCF中,BC=AF,即可得到AF+FD=BC+CG,即AD=BG=a.
解答 解:(1)∵CD的垂直平分线交CD于E,交AD于F,
∴FC=FD,
∴∠D=∠FCD=45°,
∴∠CFD=90°,即∠AFC=90°,
又∵AD∥BC,∠A=90°,
∴∠B=90°,
∴四边形ABCF是矩形,
又∵AB=BC,
∴四边形ABCF是正方形;
(2)∵FG垂直平分CD,
∴CE=DE,∠CEG=∠DEF=90°,
∵BG∥AD,
∴∠G=∠EFD,
在△CEG和△DEF中,
$\left\{\begin{array}{l}{∠G=∠EFD}\\{∠CEG=∠DEF}\\{CE=DE}\end{array}\right.$,
∴△CEG≌△DEF(AAS),
∴CG=FD,
又∵正方形ABCF中,BC=AF,
∴AF+FD=BC+CG,
∴AD=BG=a.
点评 本题主要考查了正方形的判定与性质,线段垂直平分线的性质以及全等三角形的判定与性质的综合应用,解决问题的关键是掌握:有一组邻边相等的矩形是正方形;线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
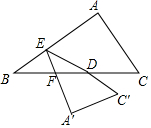 在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为$\frac{1}{2}$或$\frac{5}{4}$.
在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为$\frac{1}{2}$或$\frac{5}{4}$.
 △ABC中,AB=AC,∠BAC=120°,AD⊥BC,且AB=6cm,求AD的长.
△ABC中,AB=AC,∠BAC=120°,AD⊥BC,且AB=6cm,求AD的长.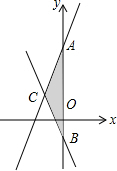 如图,已知,直线y=2x+3与直线y=-2x-1,求△ABC的面积.
如图,已知,直线y=2x+3与直线y=-2x-1,求△ABC的面积.