题目内容
13.解方程组:(1)$\left\{\begin{array}{l}{x+2y=1,①}\\{3x-2y=11②}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{m}{2}+\frac{n}{3}=13}\\{\frac{m}{3}-\frac{n}{4}=3}\end{array}\right.$.
分析 (1)根据加减消元法求解即可;
(2)先去分母变成标准形式,再根据加减消元法求解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=1,①}\\{3x-2y=11②}\end{array}\right.$
①+②得4x=12,
解得x=3,
把x=3代入①得3+2y=1,
解得y=-1.
故方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{m}{2}+\frac{n}{3}=13}\\{\frac{m}{3}-\frac{n}{4}=3}\end{array}\right.$,
去分母得$\left\{\begin{array}{l}{3m+2n=78①}\\{4m-3n=36②}\end{array}\right.$
①×3+②×2得17m=306,
解得m=18,
把m=18代入①得54+2n=78,
解得n=12.
故方程组的解为$\left\{\begin{array}{l}{m=18}\\{n=12}\end{array}\right.$.
点评 此题主要考查了解二元一次方程组的方法,要熟练掌握,注意代入法和加减法的应用.

练习册系列答案
相关题目
5.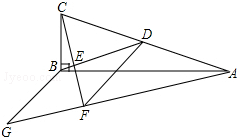 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )
 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )| A. | 9.5 | B. | 10 | C. | 12.5 | D. | 20 |
2.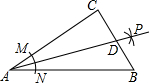 在一次数学活动课上小芳,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( )
在一次数学活动课上小芳,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( )
 在一次数学活动课上小芳,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( )
在一次数学活动课上小芳,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( )| A. | 150 | B. | 130 | C. | 240 | D. | 120 |
3.下列运算正确的是( )
| A. | (a-2)2=a2-4 | B. | a2•a4=a8 | C. | a3+a2=2a5 | D. | (-ab2)3=-a3b6 |

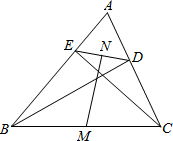 如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,取BC的中点M,DE的中点N,请你观察并猜想:MN与DE有什么样的位置关系并说明理由.
如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,取BC的中点M,DE的中点N,请你观察并猜想:MN与DE有什么样的位置关系并说明理由.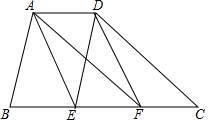 如图,在四边形ABCD中,AD∥BC,点E、F在边BC上,DE∥AB,AF∥DC,且AE∥DF.
如图,在四边形ABCD中,AD∥BC,点E、F在边BC上,DE∥AB,AF∥DC,且AE∥DF.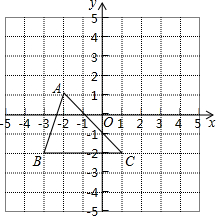 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.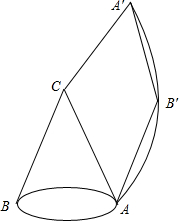 如图,沿纸筒圆锥的母线CA剪开展开,点A对应点为A′,点B对应点为B′,连接A′B′,B′A,四边形CA′B′A恰好是个菱形,若CA=6cm,则圆锥的底面积为4π(结果保留π).
如图,沿纸筒圆锥的母线CA剪开展开,点A对应点为A′,点B对应点为B′,连接A′B′,B′A,四边形CA′B′A恰好是个菱形,若CA=6cm,则圆锥的底面积为4π(结果保留π).