题目内容
5.解方程:$\frac{7x}{{x}^{2}+3x-10}$-$\frac{12}{{x}^{2}+x-6}$=$\frac{7}{x+5}$.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:方程整理得:$\frac{7x}{(x-2)(x+5)}$-$\frac{12}{(x-2)(x+3)}$=$\frac{7}{x+5}$,
方程两边都乘以最简公分母(x-2)(x+3)(x+5),得:7x(x+3)-12(x+5)=7(x-2)(x+3),
解得:x=9,
经检验:x=9是原分式方程的解,
∴分式方程的解为x=9.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
16.下列各式能用完全平方公式分解因式的是( )
| A. | x2-6x+9 | B. | 1+x2 | C. | x+2xy+1 | D. | x2+2x-1 |
14.若方程x2-4x-3=0的两实根为x1、x2,则x1+x2的值为( )
| A. | -3 | B. | 3 | C. | -4 | D. | 4 |
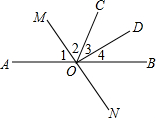 如图,直线AB,MN相交于点O,OD平分∠MON,∠1=∠2,试判断∠3与∠4之间的关系,并说明理由.
如图,直线AB,MN相交于点O,OD平分∠MON,∠1=∠2,试判断∠3与∠4之间的关系,并说明理由.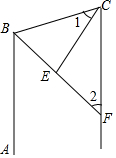 如图,∠ABC和∠BCD的平分线交于E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABC和∠BCD的平分线交于E,BE交CD于点F,∠1+∠2=90°.