题目内容
2. 小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图依次为如图所示的图形,若每个小正方形的面积为1,则该几何体的表面积为( )
小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图依次为如图所示的图形,若每个小正方形的面积为1,则该几何体的表面积为( )| A. | 10 | B. | 5 | C. | 18 | D. | 22 |
分析 由主视图可得组合几何体的底层有3列,由左视图可得该几何体有2行,由俯视图可知所以最底层有3个正方体,上面一层有1个正方体,相加可得组成组合几何体的正方体的个数.
解答 解:主视图可得组合几何体的有2列,左视图可得该几何体有2行,
由俯视图可知第一层有3个小正方体,
所以一共有5个小正方体,表面积为3×2+4×2+4×2=22.
故选:D.
点评 本题考查了由视图判断几何体;同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖”就更容易得到答案.

练习册系列答案
相关题目
12. 已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
 已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )| A. | a•b>0 | B. | a+b<0 | C. | |a|<|b| | D. | a-b>0 |
17.|-2016|等于( )
| A. | -2016 | B. | 2016 | C. | ±2016 | D. | -$\frac{1}{2016}$ |
7.在△ABC中,若∠A,∠B满足cosA=$\frac{\sqrt{3}}{2}$,∠B=45°,则∠C的大小是( )
| A. | 45° | B. | 60° | C. | 75° | D. | 105° |
14.(-2)×3的结果( )
| A. | -6 | B. | 6 | C. | 5 | D. | -5 |
11.不等式组$\left\{\begin{array}{l}{x+1>2}\\{1-x≥-2}\end{array}\right.$的解集是( )
| A. | x<1 | B. | x≥3 | C. | 1≤x<3 | D. | 1<x≤3 |
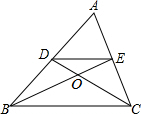 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=1:3.
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=1:3. 如图,直线y1=2x-1与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(-1,m).
如图,直线y1=2x-1与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(-1,m).