题目内容
19.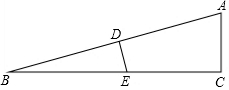 如图,△ABC中,∠C=90°,tanB=$\frac{1}{3}$,AC=2,D为AB中点,DE垂直AB交BC于E.
如图,△ABC中,∠C=90°,tanB=$\frac{1}{3}$,AC=2,D为AB中点,DE垂直AB交BC于E.(1)求AB的长度;
(2)求BE的长度.
分析 (1)首先利用正切函数的定义求得另一直角边BC的长,然后利用勾股定理即可求得AB的长;
(2)首先求得BD的长,然后求得DE的长,利用勾股定理即可求得BE的长.
解答 解:(1)∵∠C=90°,tanB=$\frac{1}{3}$,AC=2,
∴BC=2AC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{10}$;
(2)∵D为AB中点,
∴BD=$\frac{1}{2}$AB=$\sqrt{10}$,
∵DE垂直AB交BC于E,tanB=$\frac{1}{3}$,
∴DE=$\frac{1}{3}$BD=$\frac{\sqrt{10}}{3}$,
∴BE=$\sqrt{B{D}^{2}+D{E}^{2}}$=$\sqrt{(\sqrt{10})^{2}+(\frac{\sqrt{10}}{3})^{2}}$=$\frac{2\sqrt{5}}{3}$.
点评 本题考查了解直角三角形及勾股定理的知识,解题的关键是从题目中整理出直角三角形并选择合适的边角关系求得相关线段的长,难度不大,属于中等题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列现象:①用两颗钉子就可以把木条固定在墙上;
②建筑工人砌墙时,经常现在两墙立桩拉线,然后沿着砌墙;
③从A到B架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程;
⑤同等半径下,半圆的周长小于整圆的周长.
其中能体现数学事实“两点之间,线段最短”的是( )
②建筑工人砌墙时,经常现在两墙立桩拉线,然后沿着砌墙;
③从A到B架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程;
⑤同等半径下,半圆的周长小于整圆的周长.
其中能体现数学事实“两点之间,线段最短”的是( )
| A. | ①②③ | B. | ③⑤ | C. | ②④⑤ | D. | ③④⑤ |
4.如果把$\frac{5x}{x+y}$中的x与y都扩大为原来的10倍,那么这个代数式的值( )
| A. | 扩大为原来的10倍 | B. | 扩大为原来的5倍 | ||
| C. | 缩小为原来的$\frac{1}{2}$ | D. | 不变 |
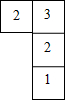 若一个几何体由几个大小相同的小正方体搭成,每个小正方体的棱长为1cm.从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数.
若一个几何体由几个大小相同的小正方体搭成,每个小正方体的棱长为1cm.从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数. 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E,⊙O的切线BF与弦AD的延长线相交于点F,且OA=3,BE=2.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E,⊙O的切线BF与弦AD的延长线相交于点F,且OA=3,BE=2.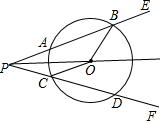 如图,已知点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D.求证:
如图,已知点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D.求证: