题目内容
18.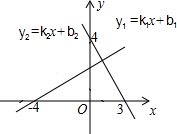 如图,直线y1=k1x+b1与坐标轴交于点(-4,0)和(0,2.9);直线y2=k2x+b2与坐标轴交于点(3,0)和(0,4).不等式组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}>0}\\{{k}_{2}x+{b}_{2}>0}\end{array}\right.$的解集是( )
如图,直线y1=k1x+b1与坐标轴交于点(-4,0)和(0,2.9);直线y2=k2x+b2与坐标轴交于点(3,0)和(0,4).不等式组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}>0}\\{{k}_{2}x+{b}_{2}>0}\end{array}\right.$的解集是( )| A. | x>-4 | B. | x<3 | C. | -4<x<3 | D. | x<-4或x>3 |
分析 先根据图象求出每个不等式的解集,再根据大小小大中间找求出它们的公共部分即可.
解答 解:∵直线y1=k1x+b1与x轴交于点(-4,0),且y随x的增大而增大,
∴不等式k1x+b1>0的解集为x>-4;
∵直线y2=k2x+b2与x轴交于点(3,0),且y随x的增大而减小,
∴不等式k2x+b2>0的解集为x<3,
∴不等式组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}>0}\\{{k}_{2}x+{b}_{2}>0}\end{array}\right.$的解集是-4<x<3.
故选C.
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了一元一次不等式组的解集.

练习册系列答案
相关题目
9.下列运算不正确的是( )
| A. | a3•a2=a5 | B. | (x3)2=x9 | C. | x5+x5=2x5 | D. | (-ab)5÷(-ab)2=-a3b3 |
13.不等式-$\frac{1}{2}$x>-1的解集为( )
| A. | x>2 | B. | x<2 | C. | x>-2 | D. | x<-2 |
 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),B(4,1).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),B(4,1).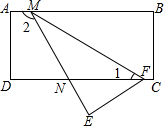 如图,将一块含有30°角的直角三角板的两个顶点叠放在长方形纸片的两条对边上,如果∠MEF=90°,∠EMF=30°,AB∥CD,∠1=28°,求∠2的度数.
如图,将一块含有30°角的直角三角板的两个顶点叠放在长方形纸片的两条对边上,如果∠MEF=90°,∠EMF=30°,AB∥CD,∠1=28°,求∠2的度数.